Why physics needs art to help picture the universe

Historians of science usually date the origin of the Scientific Revolution as 1543, when Copernicus’ De Revolutionibus first put the Earth in motion. While that is a convenient and defensible choice, it is not the only good candidate. An earlier scientific breakthrough, driven by the needs of art rather than astronomy, was equally profound: Filippo Brunelleschi’s invention of drawing in perspective, around 1420.

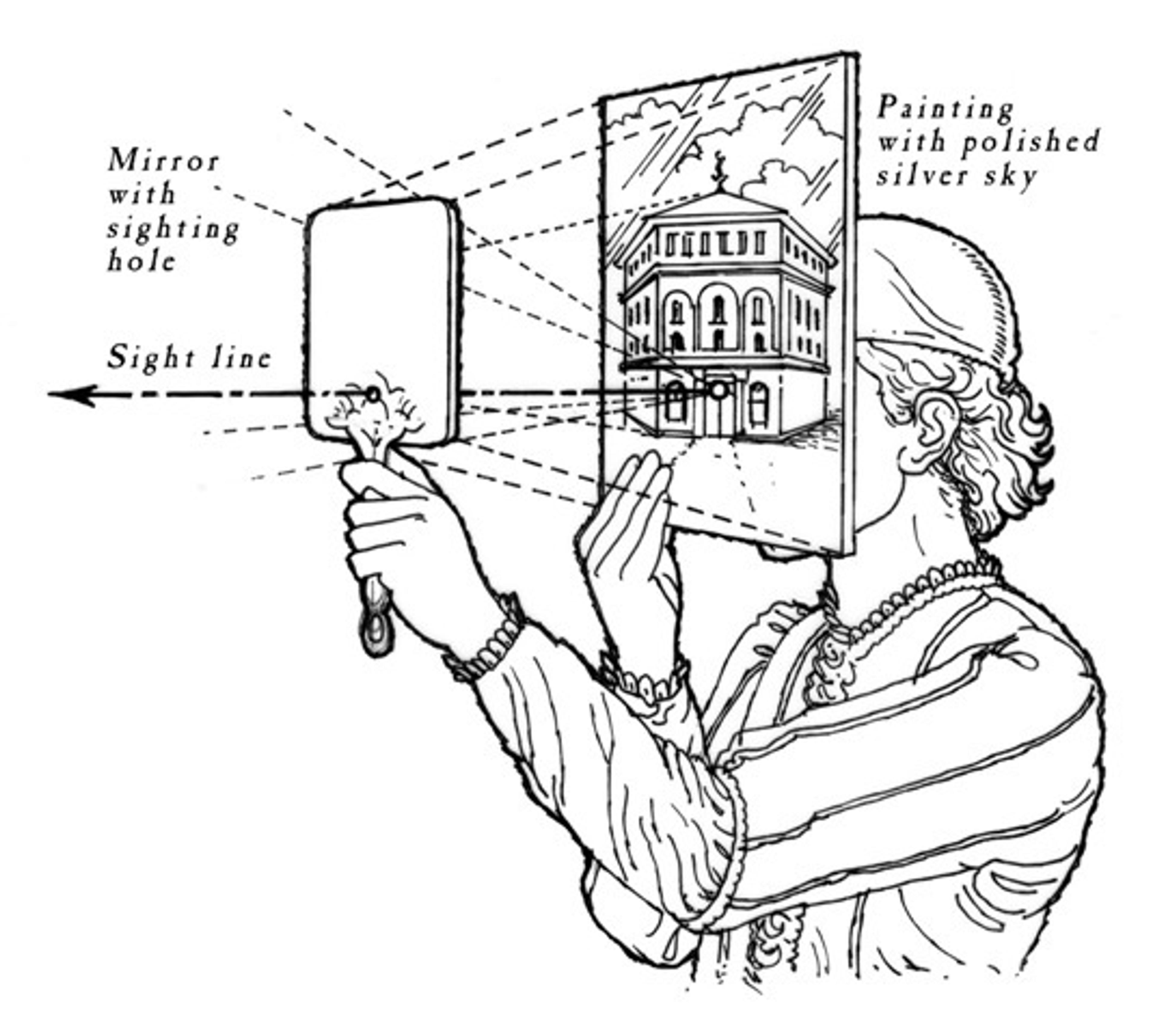
Figure 1: Brunelleschi’s arrangement allows a viewer to compare a reflected drawing to the thing itself, by removing the mirror

Brunelleschi demonstrated his ability to render scenes accurately through the brilliantly convincing experiment shown in Figure 1 below. Fifteen years later, Leon Battista Alberti published a classic explanation of the technique. It involves a fascinating new kind of geometry, projective geometry.

The work of Brunelleschi and Alberti made an enormous impact on the artists of the time. Obviously, it allowed more accurate rendering. It was also a great confidence-builder: here, at last, was a major discovery that clearly went beyond what had been achieved by the ancient Greeks and Romans. For artists, it was no longer a matter of recovering what had been lost, but of discovering a fundamentally new creative power.

We can see this reflected in such masterpieces as Perugino’s Delivery of the Keys (1481-82) in Figure 2 below. The tiles of the city square, the parallels defined by architecture, and the relative sizes of people and trees receding into the distance all afford occasions for scientifically accurate rendering.

It is sometimes said that science and art are fundamentally different in their approach and their dominion, since science strives to be objective while art is inherently subjective. The science of perspective demonstrates the superficiality of such claims. With perspective, our concern is how a scene actually looks to a particular person from a specific vantage point. It might be defined, indeed, as an objective study of subjectivity.

It is remarkable how perspective anticipates the concepts that dominate our basic understanding of Nature’s laws. Many of the central ideas of modern physics are unfamiliar to most people. They can seem abstract and forbidding if they are introduced abruptly, in the strange contexts that are their natural habitat. That’s why those of us who try to bring those ideas to a broad audience must often work in metaphors and analogies. But it’s challenging to find metaphors that are both faithful to the original ideas and readily accessible; and even more challenging to do it in a way that does justice to their beauty. I’ve struggled with that problem many times over the years. Here, I’m happy to present a solution that’s given me a real feeling of satisfaction.

The science of projective geometry, that artistic innovation of the Renaissance, contains not merely metaphors, but genuine models of big, cunning and awesomely pregnant ideas:

• Relativity is the idea that the same subject can be represented, faithfully and without loss, in many different ways. Relativity, in this sense, is the very essence of projective geometry. We can paint the same scene from many different perspectives. The dispositions of paint on canvas will be different, but all will represent the same information about the subject, just differently encoded.
• Symmetry is closely related to relativity, though our attention is directed now to the subject of the painting rather than the viewer. ‘Change Without Change’ is the essence of symmetry. Consider the most symmetric of shapes: the circle. Rotate a circle around its centre, through any angle. Such transformations change the position of each point on the circle, while the circle as a whole does not change. Similarly, if we move the subject of our painting – say by rotating it, or changing its position – we will change its appearance. But its projective description – that is, the totality of views offered by all possible perspectives – remains the same, because you can relocate your easel to compensate.
• Invariance is the counterpoint to relativity. Many aspects of the subject are represented differently, as we change perspective, but some features are common to all those representations. For example, straight lines in the subject will appear as straight lines from any perspective, though their orientation and position on the canvas will vary; and if three straight lines intersect in the subject, their representatives will still meet at a point, from any perspective. Features that are common to all representations are said to be invariant. Invariant quantities are profoundly important, because they define objective features of the subject, which are valid from any perspective. They define the essence of its ‘objective reality’.

At the frontiers of modern physics, relevant experiments are difficult. The easy ones have been done and their lessons have been thoroughly absorbed. The old Baconian model of patiently accumulating data and then using it to infer laws is no longer practical. Instead, the winning strategy has been to guess laws, derive their consequences, test them and thereby discover whether Nature chooses to use them.

If not data, what guides the guesswork? In a word, aesthetics. And it is symmetry, in the sense described above, that has been our most fruitful inspiration. We propose equations that admit many changes to their form that do not change their content.

There are, in fact, uncanny parallels between the basic symmetry principles embodied in our fundamental laws and two new varieties of artistic perspective.

In anamorphic artworks such as István Orosz’s distorted drawing of a column in Figure 3 below, one can use devices such as mirrors and lenses to go beyond the transformations of ordinary perspective. Similarly, in general relativity, a wide variety of transformations in the look of space-time can be achieved by rearranging the so‑called metric fluid. (This is the essence of Albert Einstein’s ‘general covariance’.)

Einstein arrived at his theory of gravity by finding equations whose content is unchanged by such transformations.

Our theories of the other basic forces – electromagnetism, and the weak and strong forces – are based on a kind of transformation that is less common, but not unknown, in art. Here one makes changes not by moving the points of an image, but by transforming colours in different ways at different places. Henri Matisse produced several striking images using this idea.

Today there are vibrant interactions between science and art on many fronts. A few examples: fractals have been a source of inspiration for graphic art and empowered the creation of gorgeous artificial ‘landscapes’; posters with images from space, beautifully enhanced with false colours, grace many walls; movies and sports broadcasts are rich in creative digital image processing.

But the possibilities for creative collaboration are far from exhausted. In fact, I think we’ve barely scratched the surface.

Physicists often, and rightly, extol the beauty of their concepts and equations. On the other hand, humans are intensely visual creatures. It will be fruitful to use the modern resources of signal processing and computer graphics to translate those beautiful concepts and equations into forms that the visual cortices of physicists can grasp, and that people in general can admire and enjoy. We need, in particular, better ways to put ourselves in sensory contact with spaces of high dimension, such as the ones we meet in quantum theory and when handling big data. Awesome opportunities await modern champions of Brunelleschi’s spirit.