Isaac Newton had a problem with the concept of action-at-a-distance. On one hand, like other 17th-century mechanist philosophers, he was deeply suspicious of the idea. As he wrote to the theologian Richard Bentley in 1693:
[T]hat one body may act upon another at a distance through a vacuum, without the mediation of anything else, by and through which their action and force may be conveyed from one to the other, is to me so great an absurdity, that I believe no man who has in philosophical matters a competent faculty of thinking, can ever fall into it.
On the other hand, there’s his own theory of gravity, published in his Principia several years earlier. It says that one body can exert a force on another, at arbitrary distance, without the need for any intermediary. What was a poor genius to do?
How Newton dealt with this dilemma in his own mind is still a matter for debate. Privately, his letter to Bentley continues: ‘Gravity must be caused by an agent acting constantly according to certain laws; but whether this agent be material or immaterial, I have left open to the consideration of my readers.’ In public, he seems to express disdain for the question: ‘I have not as yet been able to deduce from phenomena the reason for these properties of gravity, and I do not feign hypotheses.’
Two centuries later, Albert Einstein got Newton off the hook – though not before he’d made the problem even worse. Einstein’s 1905 theory of special relativity raised a new difficulty for Newton’s theory of gravity. Instantaneous action-at-a-distance requires that the distant effect is simultaneous with the local cause. According to special relativity, however, simultaneity is relative to the observer. Different observers disagree about which pairs of events are simultaneous, and there’s simply no fact of the matter about who is right.
Without simultaneity at a distance, the notion of instantaneous action-at-a-distance doesn’t make sense. By making Newton’s theory of gravity even more problematic, special relativity gave Einstein an extra motivation for developing his own theory. He succeeded in his theory of general relativity (GR) 10 years later. GR explains gravity in terms of the curvature of spacetime, and abandons the idea that it acts instantaneously. In GR, gravitational effects propagate at the speed of light. If the Sun suddenly vanished, it would be eight minutes before the Earth reacted.
Unfortunately for Einstein, the physics of action-at-a-distance turned out to be Whack-a-Mole. He had knocked it on the head in one place, but it popped up in another – and he deserves some of the credit for that, too. Another of Einstein’s great discoveries in 1905 – the one he thought most important – was that light can behave like individual particles, now called photons. This became one of the foundations of the new theory of quantum mechanics, developed by Erwin Schrödinger, Werner Heisenberg and others in the 1920s.
Einstein was never happy with quantum mechanics. As he complained later to Max Born, another quantum pioneer: ‘The theory cannot be reconciled with the idea that physics should represent reality in time and space, free from spooky actions at a distance.’
Einstein’s objections to quantum mechanics began very early. Schrödinger’s version of the theory introduced a new mathematical entity, the wave function, which seemed to allow the position of an unmeasured particle to be spread out across an arbitrarily large region of space. When the particle’s position was measured, the wave function was said to ‘collapse’, suddenly becoming localised where the particle was detected. Einstein objected that if this collapse was a real physical process, it would reintroduce action-at-a-distance, and so be incompatible with special relativity.
Einstein wanted to regard collapse of the wave function as a change in our information about the particle, not a change in the particle itself. Seen in this way, there is nothing surprising about it. If you know that your friend is somewhere in London and then spot her in Covent Garden, there’s a change in your knowledge but not in your friend herself. But for Einstein’s opponents – Niels Bohr and Heisenberg, among others – this view of quantum mechanics was unacceptable. They maintained that the quantum particle simply didn’t have a precise location until it was observed.
Einstein thought he had a decisive objection to Bohr and Heisenberg. He published it with two Princeton colleagues, Boris Podolsky and Nathan Rosen, in 1935. The core of the Einstein-Podolsky-Rosen (EPR) argument is the assumption of no action-at-a-distance – ie, as Einstein expressed it later, the principle that ‘the real states of spatially separate objects are independent of each other’.
‘Measurements on separated systems cannot directly influence each other – that would be magic’
Given this assumption, the EPR argument is very simple. It notes that there are cases in which, because two quantum particles have interacted in the past, a measurement on one makes a difference to the wave function of the other. The two particles concerned can be a long distance apart at this point, so the assumption of no action-at-a-distance implies that the choice of measurement on one doesn’t affect the ‘real state’ of the other. The difference it makes to the wave function of the distant particle must be a difference in our information about that particle. As with our friend who is in Covent Garden, when all we know is that she is in London, quantum particles must have properties not captured by the wave function – the quantum description must be incomplete.
The EPR argument depends on the fact that quantum mechanics allows a new kind of connection between widely separated particles. This connection is now called entanglement, a term coined by Schrödinger in 1935, who also thought it obvious that entanglement cannot allow action-at-a-distance, and that the quantum description must be incomplete: ‘Measurements on separated systems cannot directly influence each other – that would be magic.’
Schrödinger and Einstein’s view got little traction, even though – cynics might say because – the response of Bohr and his Copenhagen school to the EPR argument is famously obscure. But there are elements that remind us of Newton’s response ‘I do not feign hypotheses.’ The contemporary ‘shut-up-and-calculate’ interpretation of quantum mechanics (as the physicist David Mermin called it) denies that physics is in the business of describing a real world, in order to avoid any literal commitment to Schrödinger’s ‘magic’.
The really bad news for Einstein came not from Copenhagen but from Belfast, from the ingenious brain of John Stewart Bell. Bell was no fan of the Copenhagen view – he saw the appeal and power of the EPR argument – but by pressing further on the same kind of two-particle experiments, he derived what seemed an insuperable difficulty for Einstein. Einstein’s argument took for granted that there is no action-at-a-distance, but Bell’s Theorem (1965) seemed to show that quantum theory requires it.
The theorem turns on Einstein’s own discovery that many phenomena in the quantum world show a kind of ‘discreteness’ not present in classical physics. Bell considered the correlations between such discrete, either/or events in two-particle experiments like those of EPR. A typical EPR-Bell experiment, as they are now called, is performed with pairs of photons produced at a common source. The photons fly in opposite directions into measurement boxes controlled by everybody’s favourite thought-experimenters, Alice and Bob. Alice and Bob can choose one of several setting angles for their measurement boxes, and each box produces one of two outputs for each, ie, a detection of the photon on one of two possible channels.
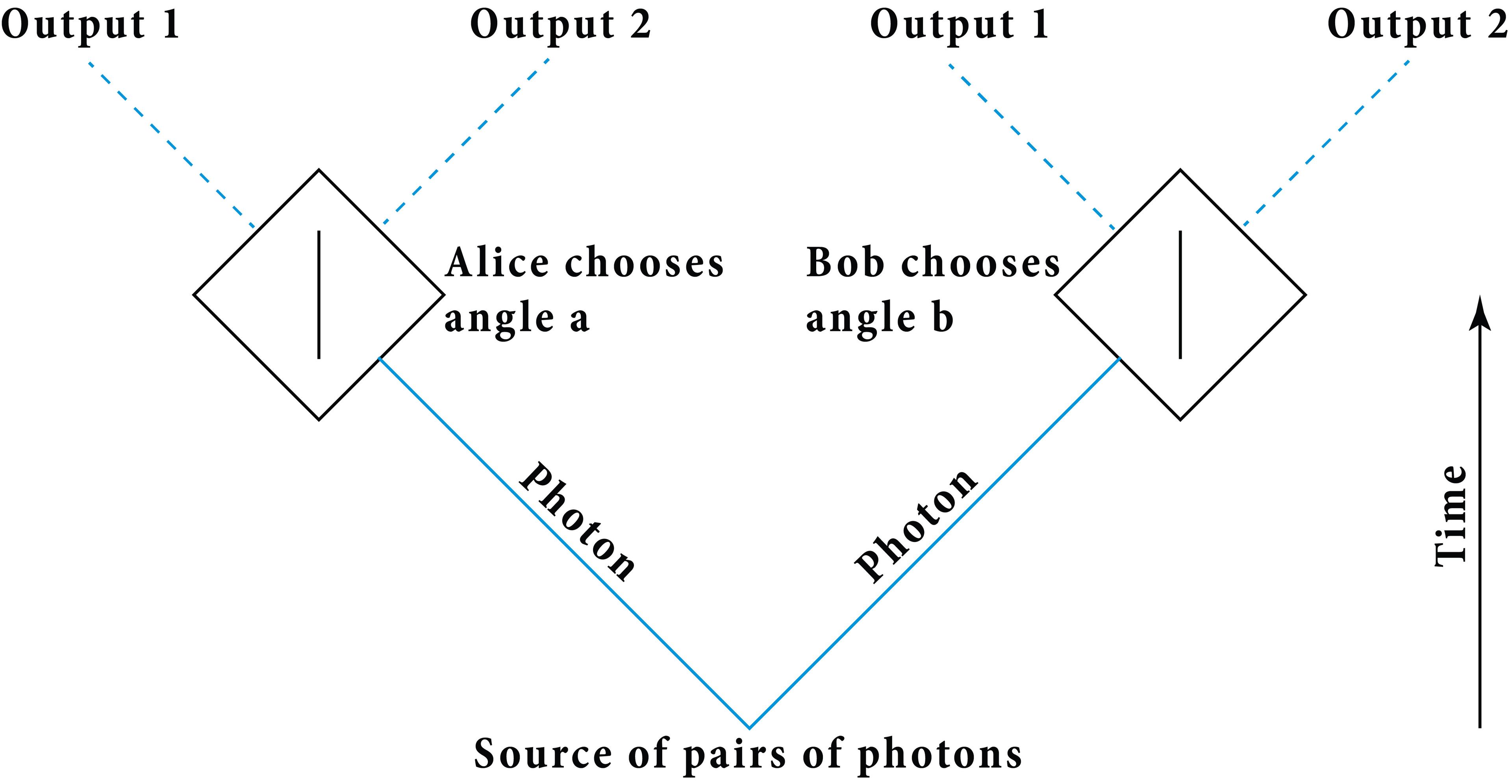
Diagram 1: An EPR-Bell experiment
Quantum mechanics predicts that, if the experiment is repeated many times, there will be correlations between the results on Alice’s side and on Bob’s side. These correlations depend on whether Alice and Bob choose the same or different angles – more precisely, they depend on the difference between the two angles. Bell’s brilliance was to see that these correlations are deeply puzzling. They imply that Bob’s photon must somehow know what Alice chooses, and vice versa, even though the two experiments can be far apart. This seems to be action-at-a-distance – the very option that Einstein had assumed he could ignore in simpler versions of the experiment.
The core of Bell’s argument can be explained using analogies. Consider what we’ll call the ‘Gemini game’. Pairs of twins are separated, and each is randomly offered one of three coloured cards: red, yellow or blue. Each twin has to accept or decline the card. If they choose differently when offered the same coloured card, they are immediately disqualified. Otherwise, their objective is just to choose differently when offered different coloured cards, as often as possible.
The twins don’t know in advance what cards each of them will be offered, nor what card the other is being offered, in any particular instance. So, to avoid disqualification, they need a policy – eg, ‘Accept red, decline yellow and blue.’ Because there are three cards and only two options (accept or decline), any such policy recommends the same action for at least two different cards – in this case, for yellow and for blue.
There are six ways in which the twins can be shown different cards (three possibilities for Twin 1, and for each of those, two different possibilities for Twin 2). Because any policy recommends the same option for at least two cards, it will tell the twins to do the same thing in at least two of these six situations; in our example, when Twin 1 gets yellow and Twin 2 gets blue, and vice versa. This means that the best the twins can do in their attempt to choose different options when shown different cards is four out of six, or about 67 per cent, on average. This result is what’s now known as Bell’s Inequality.
The consensus is that Einstein can’t have what he wanted – a real world in space and time, without action-at-a-distance
Bell’s insight was to notice that somehow the quantum world manages to escape this inequality. Quantum particles can do something that even the most intelligent human twins cannot. Playing an equivalent game, for example, photons can get a success rate of 75 per cent. In the Gemini game, we assumed that neither twin knows what colour card the other is offered. Bell reasoned that for quantum particles to do better – to violate Bell’s Inequality – the equivalent assumption must fail in quantum mechanics. In some sense, each particle must ‘know’ what measurement is being made on the other. That ‘knowledge’ is the action-at-a-distance.
The implications of Bell’s result remain disputed. Some claim that it shows quantum mechanics implies action-at-a-distance, period. Others maintain that we can still avoid action-at-a-distance by denying that quantum mechanics is a theory about a reality in space and time. Either way, the consensus is that Einstein can’t have what he wanted – a real world in space and time, without action-at-a-distance. And many theorists, including Bell, conclude that the inequality reveals a deep tension between quantum mechanics and special relativity, the two pillars of 20th-century physics.
Over the past forty years, a lot of ingenuity has gone into designing experiments to test the quantum predictions on which Bell’s result depends. Quantum mechanics has passed them all with flying colours. Just last year, three new experiments claimed to close almost all the remaining loopholes. ‘The most rigorous test of quantum theory ever carried out has confirmed that the “spooky action-at-a-distance” that [Einstein] famously hated… is an inherent part of the quantum world,’ as Nature put it.
Newton once remarked that if he’d seen further than his predecessors, it was because he stood on the shoulders of giants. For the would-be Newtons of the present century, replicating that feat has become newly challenging. It is not just that you need to be a genius to scale such heights. With Newton, Einstein and Schrödinger huddled on one side, and Bell on the other, the shoulders of the giants now seem seriously out of line.
The surprising news is that there’s a simple and elegant solution to the problem – an option that Bell himself missed, apparently, because he confused it for something else. With Bell’s authority behind it, the confusion persists to this day, and the solution goes almost unnoticed. Yet if it works, it explains Bell’s correlations without Schrödinger’s ‘magic’ and it gets our giants back in line. Quantum mechanics no longer seems in tension with special relativity, and Bell can agree with Newton, Einstein and Schrödinger that there is no action at a distance.
This reconciliation begins with a suggestion first made by a young Parisian graduate student, Olivier Costa de Beauregard, in the late 1940s. He was a student of Louis de Broglie, a pioneer of quantum mechanics who, like Einstein and Schrödinger, was attracted to the idea that the theory is incomplete. Initially, Costa de Beauregard thought he had an objection to the EPR argument. Einstein had assumed that Alice’s measurement couldn’t affect the result of Bob’s experiment, because that would be action-at-a-distance. Costa de Beauregard pointed out that Alice could affect Bob’s particle without action-at-a-distance, if the influence followed an indirect, zigzag path through space and time, via the point in the past where the two particles intersect. But there are no zigzags like that in standard quantum mechanics, so if we put them in we are actually agreeing with Einstein that the theory is incomplete.
Later, when Bell’s work appeared, Costa de Beauregard recognised the deeper significance of the zigzag: it offers a potential reconciliation between Bell and Einstein. Bell’s argument depends on the assumption that the choice of measurement settings at the two sides of the experiment is independent of any earlier properties, or ‘hidden variables’, of the particles. This assumption is called statistical independence, but the Parisian zigzag gives us a reason to reject it.
Bell didn’t see the difference between the two proposals, and threw out the retrocausal baby with the superdeterminist bathwater
Following the setup shown in the EPR diagram above, Costa de Beauregard proposes that Alice’s choice of a measurement setting makes a difference to her particle before it arrives at the measuring device – it causes her particle to have one hidden variable rather than another at that stage. This in turn makes a difference to Bob’s particle as well as to where the particles meet, and so explains how Alice’s choice can affect Bob’s side of the experiment, even without action-at-a-distance. It is easy to explain the correlations that Bell took to imply action-at-a-distance if we allow such ‘retro’ causality.
Bell himself knew that we don’t need action-at-a-distance if statistical independence fails. So why are we all told that Bell’s Theorem shows Einstein was wrong about spooky action-at-a-distance? Why is Costa de Beauregard’s alternative simply overlooked?
There’s a clue in a letter that Bell wrote to one of us in 1988. Huw Price was a young philosopher in Sydney at the time, and plucked up the courage to send Bell two of his early papers about this retrocausal idea. Bell kindly wrote back, saying: ‘When I try to think of [backward causation] I lapse quickly into fatalism’ and referred to a published discussion for ‘what little I can say’ about the matter. However, the published discussion is about an entirely different way of rejecting Bell’s statistical independence assumption, an idea that Bell called superdeterminism. In fact, he had good reasons to reject superdeterminism. But he didn’t see the difference between the two proposals, apparently, and threw out the retrocausal baby with the superdeterminist bathwater.
To clear up this decades-old confusion, let’s begin with the familiar point that correlation need not imply causation. Furry tongues are often correlated with headaches, but neither is a cause of the other. They are correlated because they are both effects of the same cause in the past – excessive drinking. An important rule, known to philosophers as Reichenbach’s Common Cause Principle, tells us that where we find correlation without direct causation, we should look for a common cause. The qualification is crucial. Excessive drinking is correlated with headaches, but drinking causes headaches, so we don’t need to look for some third thing that causes both.
What does this rule tell us if we apply it to the hypothesis that there is a correlation between Alice’s choice of measurement settings and the properties of a particle that is making its way towards her measuring device? Superdeterminism assumes that it tells us to look for something in the past to be a common cause of Alice’s choice of measurement settings and of the relevant hidden variables of the particle. But now we have two problems.
First, what kind of common cause could have this strange combination of effects? We could replace Alice with many other ways of choosing measurement settings; for instance, as Bell suggests, we could let the Swiss lottery machine do it. The common cause would need to control that, too, according to this proposal. Second, and in Bell’s view even worse, this common cause would be deeply in tension with the belief that we (or Alice) are free to choose whatever setting we like. This is how Bell put it in 1985:
One of the ways of understanding this business is to say that the world is super-deterministic. That not only is inanimate nature deterministic, but we, the experimenters who imagine we can choose to do one experiment rather than another, are also determined. … In the analysis it is assumed that free will is genuine, and as a result of that one finds that the intervention of the experimenter at one point has to have consequences at a remote point in a way that influences restricted by the finite velocity of light would not permit. If the experimenter is not free to make this intervention, if that also is determined in advance, the difficulty disappears.
Bell’s concern about fatalism survives to this day. The option of rejecting statistical independence is commonly called the freedom-of-choice loophole. In a recent paper, Anton Zeilinger – one of the giants of experimental quantum theory – and his coauthors write that ‘the freedom-of-choice loophole refers to the requirement, formulated by Bell, that the setting choices are “free or random”.’
Three decades of worrying about free will turn out to have been a complete red herring
However, this issue about free will stems from the superdeterminist’s assumption that a correlation between measurement settings and pre-measurement hidden variables of the particle needs a common cause – and that’s simply a mistake. We need common causes in the case of furry tongues and headaches, where neither of two correlated events is a cause of the other. But according to the Parisian zigzag, the choice of measurement settings is a cause of the pre-measurement hidden variables. We don’t need a common cause, and three decades of worrying about free will turn out to have been a complete red herring.
In his paper, Zeilinger mentions a proposal to restrict the freedom-of-choice loophole by letting measurement decisions be determined by chance events in distant galaxies, making it even more unlikely that there could be a common cause. This proposal, and the elaborate experimental programme now based on it, rest on the same mistake: we don’t need a common cause, and won’t learn anything by going to all this trouble to rule one out.
With superdeterminism filed for posterity where it belongs – under ‘Even giants make mistakes’ – it is easy to read Bell’s Theorem as an argument for retrocausality. The argument shows that quantum mechanics implies that the alternative to retrocausality is action-at-a-distance. But ‘that would be magic’, as Schrödinger put it, and it conflicts with special relativity. So retrocausality it should be.
At this point, some readers may feel that, while action-at-a-distance is peculiar, it’s not half as odd as the present affecting the past. Retrocausality suggests the kind of paradoxes familiar from time-travel stories. If we could affect the past, couldn’t we signal to our ancestors in some way that would prevent our own existence? Luckily for the Paris option, it turns out that the kind of subtle retrocausality needed to explain Bell’s correlations doesn’t have to have such consequences. In simple cases, we can see that it couldn’t be used to signal, for the same reason that entanglement itself can’t be used to signal. But first, let’s consider a couple of other objections that critics raise at this point.
Physicists sometimes object that if retrocausality can’t be used to signal then it doesn’t have any experimental consequences. We physicists are interested in testable hypotheses, everything else is mere philosophy, they proclaim (using ‘philosophy’ in its pejorative sense!). But retrocausality offers an explanation of the results of all the standard experimental tests of the Bell correlations. If it works, it is confirmed by these experiments just as much as action-at-a-distance is confirmed. Experiments alone won’t distinguish between the two proposals, but this is no more a reason for ignoring retrocausality than it is for ignoring action-at-a-distance. The choice between the two needs to be made on other grounds – eg, on the basis that retrocausality is easier to reconcile with special relativity.
Either way, the result will be that our naive picture of time needs to be revised in the light of a new understanding of physics
Some readers may raise a more global objection to retrocausality. Ordinarily, we think that the past is fixed while the future is open, or partly so. Doesn’t our freedom to affect the future depend on this openness? How could we affect what was already fixed? These are deep philosophical waters, but we don’t have to paddle out very far to see that we have some options. We can say that, according to the retrocausal proposal, quantum theory shows that the division between what is fixed and what is open doesn’t line up neatly with the distinction between past and future. Some of the past turns out to be open, too, in whatever sense the future is open.
To understand what sense that is, we’d need to swim out a lot further. Is the openness ‘out there in the world’, or is it a matter of our own viewpoint as agents, making up our minds how to act? Fortunately, we don’t really need an answer: whatever works for the future will work for the past, too. Either way, the result will be that our naive picture of time needs to be revised in the light of a new understanding of physics – a surprising conclusion, perhaps, but hardly a revolutionary one, more than a century after special relativity wrought its own changes on our understanding of space and time.
Still, we we want to explain why the kind of retrocausality involved in the Parisian zigzag needn’t allow us to send signals to the past. We are going to do this by examining an experiment in which standard quantum mechanics predicts the mirror-image: the same subtle causality directed to the future, achieved without signalling to the future.
We begin with the earlier EPR-Bell experiment. Let’s put it in a mirror, as shown below. The mirror flips Alice’s half of the experiment in time, so that it now looks like an experiment in which a photon enters through one of the two channels at the bottom and leaves through the channel on the top right, heading in the direction of Bob’s measuring device. If we combine the mirror image of Alice’s side with the original version of Bob’s side, we get a diagram of an experiment done with one photon, travelling left to right, from the reflection of Alice’s device to Bob’s device. Let’s call the reflection of Alice ‘Ecila’, to remind us that she is Alice in reverse.
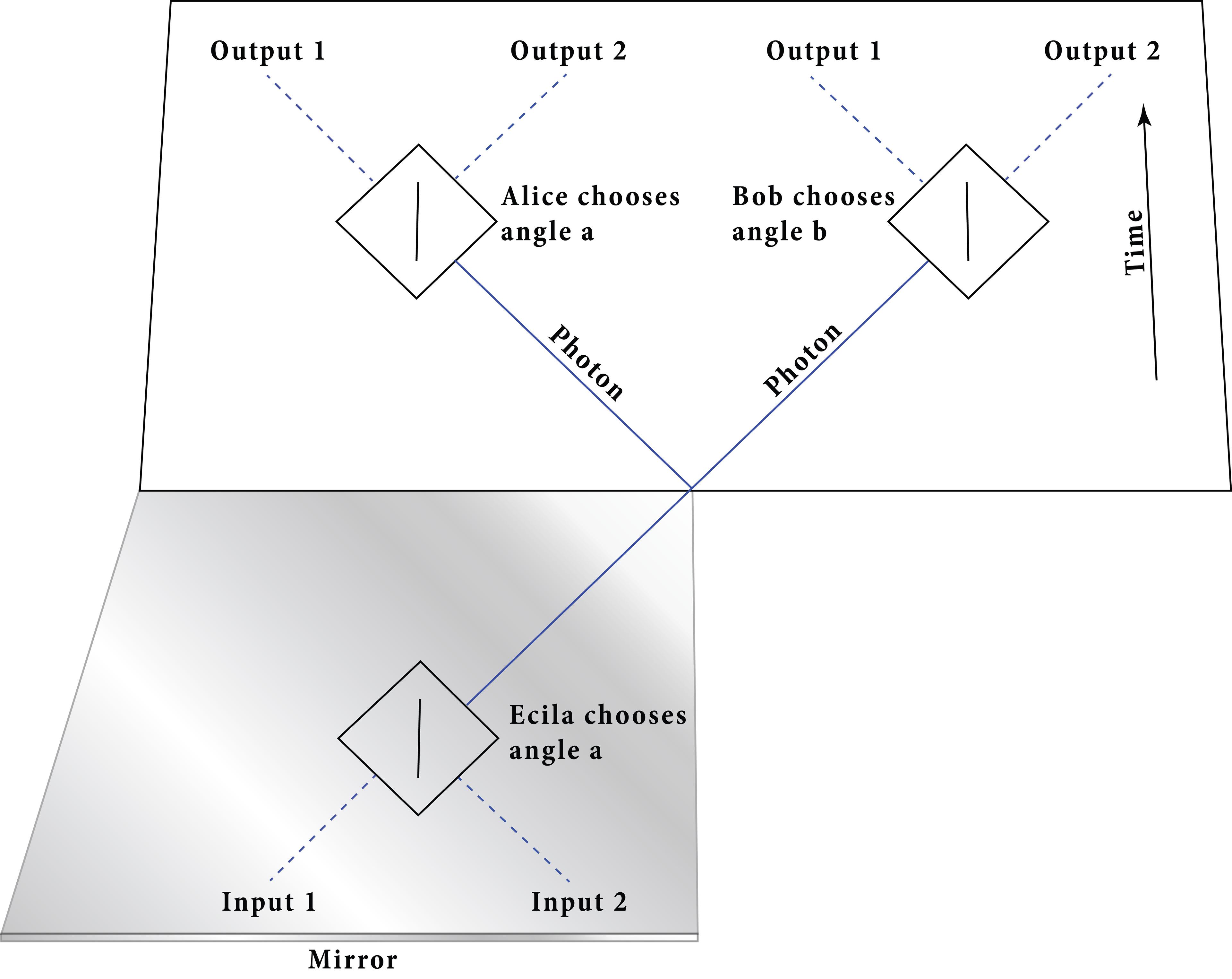
Figure 2. Alice through the looking glass
This use of the mirror isn’t a trick. Throwing out Alice’s upper-left corner, the remaining experiment is one we can actually perform, using only a single photon. The underlying physics of the original experiment ensures that using the mirror is completely kosher. It ensures that the correlations between Ecila and Bob in the new experiment are exactly the same as the Bell correlations between Alice and Bob in the original experiment.
In the original experiment, each output corresponds to one type of polarisation – the orientation of the vibration of the photon, analogous to the angle at which a guitar string is vibrating. The outcomes on each side are discrete: after passing through the box that represents a ‘polariser’ (which admits only one type of vibration) and being measured, the photon is always found on one channel or the other. The outputs are also completely random from the point of view of Alice or Bob individually. There are correlations when they compare notes but, until they do that, they might as well just be tossing a coin.
To make the new experiment a faithful mirror image on the left, Ecila’s inputs need to be discrete and random in the same way. In other words, we need to assume that there’s a photon arriving on one channel or the other, but which channel is completely unpredictable. For simplicity, let’s give this job to a demon – a random-acting agent. The demon does exactly what ‘Nature’ does at both ends of the experiment except in reverse, so let’s call her ‘Erutan’. Alice doesn’t know Nature’s choice in advance, so we stipulate that Ecila doesn’t know Erutan’s choice either.
Standard quantum mechanics tells us that, despite Erutan, Ecila has a lot of control over the photon as it leaves her side of the experiment. Ecila controls the polarisation of the photon almost completely by choosing the setting of her polariser. To be precise, she can fix the polarisation to one of two values, differing by 90 degrees. Erutan gets the final choice between those two values by choosing which way the photon enters the box.
We stress two things about Ecila’s control of the photon’s polarisation. First, it’s a consequence of the discreteness condition, the stipulation that Erutan has to supply a photon on one channel or the other. If we do the same experiment in classical physics, Erutan can produce whatever polarisation she likes, taking away Ecila’s ability to control anything. Second, Ecila can’t signal to Bob, despite her control of the photon’s polarisation. It’s as though Erutan is tossing a series of coins, and Ecila – without looking – is deciding whether each one should be turned over before it’s sent to Bob. Ecila’s choices make a difference to the sequence of heads and tails that Bob receives, but the sequence looks completely random (ie, message-free) from his point of view.
we can emerge from the looking glass and apply the same lessons to the Parisian zigzag
We’ve learnt two things from Ecila and Erutan. First, the discreteness condition gives Ecila a new kind of forward control in standard quantum mechanics. Second, this new control can’t be used to signal, even though it surely counts as causation.
With these points in mind, we can emerge from the looking glass and apply the same lessons to the Parisian zigzag. Costa de Beauregard’s proposal is that Alice has the same control over the photon before it reaches her polariser as Ecila has over the photon after it leaves her polariser, according to standard quantum mechanics. This control will be enough to explain the correlations in the two-photon experiment, just as in the one-photon experiment; the physics behind the mirror will guarantee that. And because nature behaves just like Erutan, this control will be real enough to count as causation – Alice is making a genuine difference to the photon – but not strong enough to let Alice signal Bob.
In the two-photon case, no one would give this control to Alice without giving it to Bob too. That would be a ridiculous left/right asymmetry, not to mention female/male asymmetry! So the Paris proposal is that Bob, too, has a degree of control over his photon before it reaches his polariser. If we add this to the one-photon experiment, it has a similar benefit: it gets rid of a time-asymmetry between Ecila and Bob.
Now at last we get to the heart of the new argument for retrocausality in the quantum world. It turns on the fact that physics doesn’t seem to care about the direction of time. If the laws allow a physical process, they also allow the same process running in reverse. This isn’t true of many everyday processes – eggs turn into omelettes, but not the reverse! – but that seems to be a result of large-scale statistical effects associated with the second law of thermodynamics. At the fundamental level, there is no way to tell whether a video of physical processes is being played forwards or backwards.
Let’s apply this time symmetry to our one-photon experiment with Erutan and Ecila at one end, Bob and Nature at the other. We chose Erutan so that she behaves like Nature in reverse. If we reverse a video of the experiment, nothing changes at the two ends; Nature in reverse looks like Erutan, and Erutan in reverse looks like Nature. But if Ecila is affecting the photon between the polarisers and Bob isn’t, then reversing the video does make a difference there. In the reverse video, the photon seems controlled from the future, not from the past. If we want our theory to pass the test for time-symmetry, we’ll have to allow that Bob controls the photon too. In other words, we need retrocausality.
Notice the role of quantum discreteness. Without it, Ecila has no control over the photon, and so we can pass the test for time-symmetry without giving Bob any control either. Classical theory can be time-symmetric without retrocausality. But the quantum discreteness discovered by Einstein – and at the heart of Bell’s Theorem – makes a big difference. In combination with a commitment to time-symmetry, it gives a new reason to think that there’s a subtle kind of retrocausality built into the quantum world.
you can’t insist that Bell showed Newton, Einstein and Schrödinger to be wrong until you explain why the Paris solution won’t work
We now have two reasons for taking retrocausality seriously. First, it offers an elegant explanation of the Bell correlations, one that avoids action-at-a-distance and that allows quantum mechanics to play nicely with special relativity. Second, retrocausality preserves time-symmetry in the one-photon experiment. Both reasons turn on discreteness. It is not much of an exaggeration to say that the two experiments are really the same experiment, just differently arranged in space and time. Arranged with two photons, the cost of ignoring retrocausality is action-at-a-distance. Arranged with one photon, the cost of ignoring it is time-asymmetry. Two different ‘bads’ with the same take-home message: we should all be doing the Parisian zigzag!
At this point, defenders of other views of quantum mechanics will point out, rightly, that the zigzag idea is just a proposal; there isn’t yet a well-developed model of how to implement it. They will also insist that Parisian elegance is not compulsory. If you wish, you can choose to live with action-at-a-distance, or time-asymmetry, or shut-up-and-calculate-and-don’t-think-about-reality.
To this we say: of course, elegance is no more compulsory in science than it is in everyday life. We don’t claim that retrocausality is the only option, just that no one can insist that Bell has shown that Newton, Einstein and Schrödinger were wrong about action-at-a-distance until they explain why the Paris solution won’t work.
So, dear reader, the next time you read that Einstein has been refuted, or that action-at-a-distance has been experimentally proven, check to see whether the authors have considered the Parisian zigzag. Probably not, since it hasn’t been touched at all by the clever recent physics experiments. In that case, they have more work to do. They need some arguments against Costa de Beauregard’s proposal. On our side, we need some well-developed models of how to provide retrocausal foundations for quantum mechanics. And on both sides of the fence, surely, we owe it to all those giants to try to sort this out.






