Just what is information? For such an intuitive idea, its precise nature proved remarkably hard to pin down. For centuries, it seemed to hover somewhere in a half-world between the visible and the unseen, the physical and the evanescent, the enduring medium and its fleeting message. It haunted the ancients as much as it did Claude Shannon and his Bell Labs colleagues in New York and New Jersey, who were trying to engirdle the world with wires and telecoms cables in the mid-20th century.
Shannon – mathematician, American, jazz fanatic, juggling enthusiast – is the founder of information theory, and the architect of our digital world. It was Shannon’s paper ‘A Mathematical Theory of Communication’ (1948) that introduced the bit, an objective measure of how much information a message contains. It was Shannon who explained that every communications system – from telegraphs to television, and ultimately DNA to the internet – has the same basic structure. And it was Shannon who showed that any message could be compressed and transmitted via a binary code of 0s and 1s, with near-perfect accuracy, a notion that was previously pegged as hopelessly utopian. As one of Shannon’s colleagues marvelled: ‘How he got that insight, how he even came to believe such a thing, I don’t know.’
These discoveries were scientific triumphs. But in another way, they brought the thinking about information full-circle. Before it was the province of natural scientists, ‘information’ was a concept explored by poets, orators and philosophers. And while Shannon was a mathematician and engineer by training, he shared with these early investigators a fascination with language.
In the Aeneid, for example, the Roman poet Virgil describes the vast cave inhabited by the god Vulcan and his worker-drones the Cyclopes, in which the lightning bolt of Jupiter is informatum – forged or given shape beneath their hammers. To in-form meant to give a shape to matter, to fit it to an ideal type; informatio was the shape given. It’s in this sense that Cicero spoke of the arts by which young people are ‘informed in their humanity’, and in which the Church Father Tertullian calls Moses populi informator, the shaper of the people.
From the Middle Ages onwards, this form-giving aspect of information slowly gave way, and it acquired a different, more earthy complexion. For the medieval scholastics, it became a quintessentially human act; information was about the manipulation of matter already on Earth, as distinct from the singular creativity of the Creator Himself. Thomas Aquinas said that the intellect and the virtues – but also the senses – needed to be informed, enriched, stimulated. The scientific revolution went on to cement these perceptible and grounded features of information, in preference to its more divine and form-giving aspects. When we read Francis Bacon on ‘the informations of the senses’, or hear John Locke claim that ‘our senses inform us’, we feel like we’re on familiar ground. As the scholar John Durham Peters wrote in 1988: ‘Under the tutelage of empiricism, information gradually moved from structure to stuff, from form to substance, from intellectual order to sensory impulses.’
It was as the study of the senses that a dedicated science of information finally began to stir. While Lord Kelvin was timing the speed of telegraph signals in the 1850s – using mechanisms rigged with magnets, mirrors, metal coils and cocoon silk – Hermann von Helmholtz was electrifying frog muscles to test the firing of animal nerves. And as information became electric, the object of study became the boundary between the hard world of physics and the elusive nature of the messages carried in wires.
In the first half of the 20th century, the torch passed to Bell Labs in the United States, the pioneering communications company that traced its origins to Alexander Graham Bell. Shannon joined in 1941, to work on fire control and cryptography during the Second World War. Outside of wartime, most of the Labs’ engineers and scientists were tasked with taking care of the US’ transcontinental telephone and telegraph network. But the lines were coming under strain as the human appetite for interaction pushed the Bell system to go further and faster, and to transmit messages of ever-higher quality. A fundamental challenge for communication-at-a-distance was ‘noise’, unintended fluctuations that could distort the quality of the signal at some point between the sender and receiver. Conventional wisdom held that transmitting information was like transmitting power, and so the best solution was essentially to shout more loudly – accepting noise as a fact of life, and expensively and precariously pumping out a more powerful signal.
The information value of a message depends on the range of alternatives killed off in its choosing
But some people at the Labs thought the solution lay elsewhere. Thanks to its government-guaranteed monopoly, the Labs had the leeway to invest in basic theoretical research, even if the impact on communications technology many years in the future. As the engineer Henry Pollak told us in an interview: ‘When I first came, there was the philosophy: look, what you’re doing might not be important for 10 years or 20 years, but that’s fine, we’ll be there then.’ As a member of the Labs’ free-floating mathematics group, after the war Shannon found that he could follow his curiosity wherever it led: ‘I had freedom to do anything I wanted from almost the day I started. They never told me what to work on.’
In this spirit, a number of Bell Labs mathematicians and engineers turned from telegraphs and telephones to the more fundamental matter of the nature of information itself. They began to think about information as measuring a kind of freedom of choice, in which the content of a communication is tied to the range of what it excluded. In 1924, the Labs engineer Harry Nyquist used this line of reasoning to show how to increase the speed of telegraphy. Three years later, his colleague Ralph Hartley took those results to a higher level of abstraction, describing how sending any message amounts to making a selection from a pool of possible symbols. We can watch this rolling process of elimination at work even in such a simple sentence as ‘Apples are red’, Hartley said: ‘the first word eliminated other kinds of fruit and all other objects in general. The second directs attention to some property or condition of apples, and the third eliminates other possible colours.’
On this view, the information value of a message depends in part on the range of alternatives that were killed off in its choosing. Symbols chosen from a larger vocabulary of options carry more information than symbols chosen from a smaller vocabulary, because the choice eliminates a greater number of alternatives. This means that the amount of information transmitted is essentially a function of three things: the size of the set of possible symbols, the number of symbols sent per second, and the length of the message. The search for order, for structure and form in the wending catacombs of global communications had begun in earnest.
Enter Shannon’s 1948 paper, later dubbed ‘the Magna Carta of the Information Age’ by Scientific American. Although the theoretical merits of Shannon’s breakthrough were recognised immediately, its practical fruits would come to ripen only over the following decades. Strictly speaking, it wasn’t necessary to solve the immediate problem of placing a long-distance call, or even required for the unveiling of the first transatlantic telephone cable in 1956. But it would be necessary for solving the 1990 problem of transmitting a photograph from the edge of the solar system back to Earth across 4 billion miles of void, or for addressing the 2017 problem of streaming a video on a computer that fits in your pocket.

Claude Shannon. Photo courtesy Nokia Bell Labs
A clue to the origins of Shannon’s genius can be found in the sheer scope of his intellectual interests. He was a peculiar sort of engineer – one known for juggling and riding a unicycle through Bell Labs’ corridors, and whose creations included a flame-throwing trumpet, a calculator called ‘THROBAC’ that operated in Roman numerals (short for ‘Thrifty Roman-Numeral Backward-Looking Computer’), and a mechanical mouse named Theseus that could locate a piece of metallic cheese in a maze. Genetics, artificial intelligence, computer chess, jazz clarinet and amateur poetry numbered among his other pursuits. Some of these predated his work on information theory, while he turned to others later in life. But what remained constant was Shannon’s ability to be as captivated by the capering spectacle of life and language as he was by physics and numbers. Information had begun, after all, as a philosophical term of art, and getting at its foundations entailed just the sort of questions we might expect a linguist or a philosopher to take up.
Shannon’s ‘mathematical theory’ sets out two big ideas. The first is that information is probabilistic. We should begin by grasping that information is a measure of the uncertainty we overcome, Shannon said – which we might also call surprise. What determines this uncertainty is not just the size of the symbol vocabulary, as Nyquist and Hartley thought. It’s also about the odds that any given symbol will be chosen. Take the example of a coin-toss, the simplest thing Shannon could come up with as a ‘source’ of information. A fair coin carries two choices with equal odds; we could say that such a coin, or any ‘device with two stable positions’, stores one binary digit of information. Or, using an abbreviation suggested by one of Shannon’s co-workers, we could say that it stores one bit.
But the crucial step came next. Shannon pointed out that most of our messages are not like fair coins. They are like weighted coins. A biased coin carries less than one bit of information, because the result of any flip is less surprising. Shannon illustrated the point with this graph. You see that the amount of information conveyed by our coin flip (on the y-axis) reaches its apex when the odds are 50-50, represented as 0.5 on the x-axis; but as the outcome grows more predictable in either direction depending on the size of the bias, the information carried by the coin steadily declines.
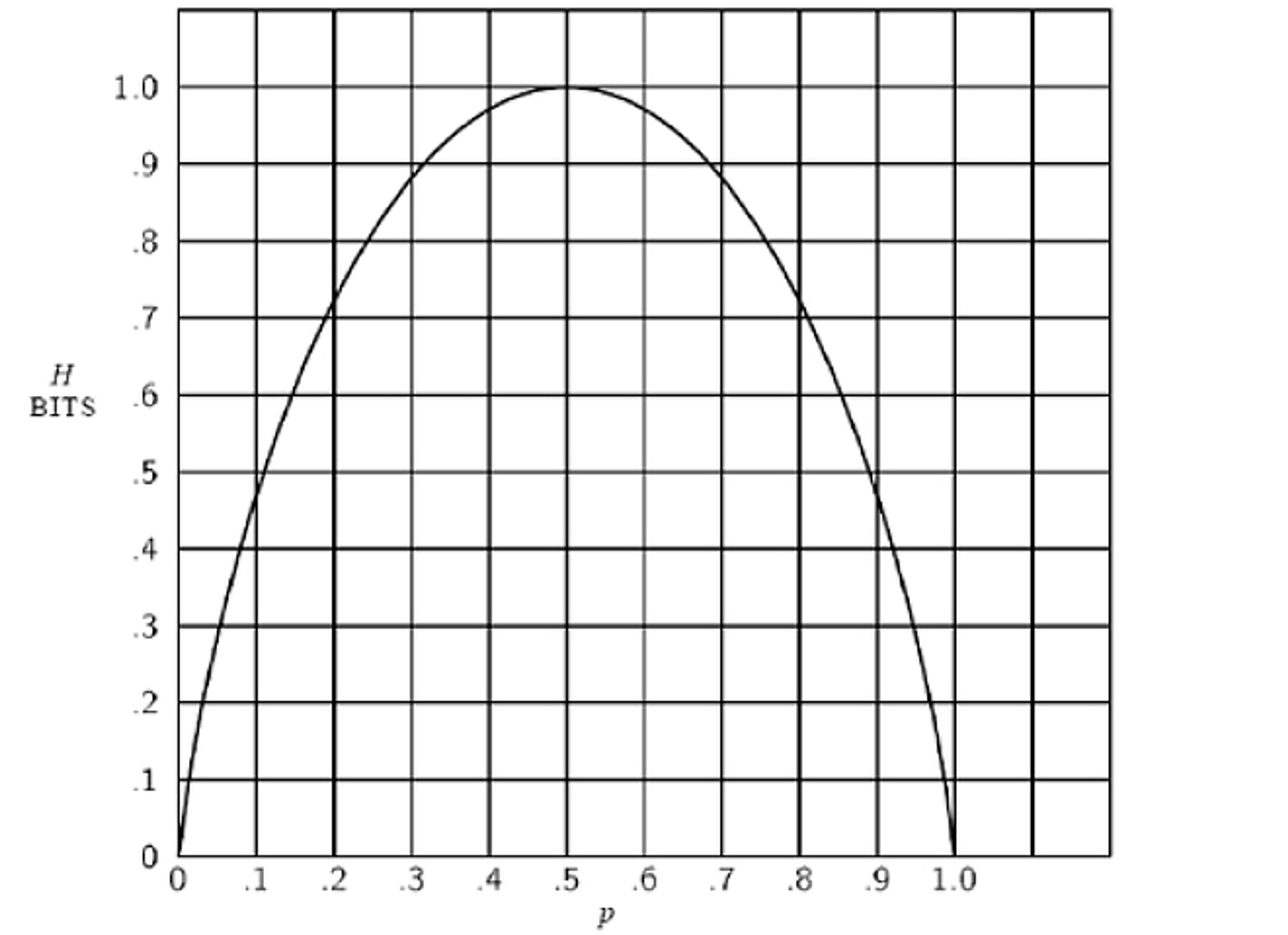
The messages humans send are more like weighted coins than unweighted coins, because the symbols we use aren’t chosen at random, but depend in probabilistic ways on what preceded them. In images that resemble something other than TV static, dark pixels are more likely to appear next to dark pixels, and light next to light. In written messages that are something other than random strings of text, each letter has a kind of ‘pull’ on the letters that follow it.
This is where language enters the picture as a key conceptual tool. Language is a perfect illustration of this rich interplay between predictability and surprise. We communicate with one another by making ourselves predictable, within certain limits. Put another way, the difference between random nonsense and a recognisable language is the presence of rules that reduce surprise.
Shannon demonstrated this point in the paper by doing an informal experiment in ‘machine-generated text’, playing with probabilities to create something resembling the English language from scratch. He opened a book of random numbers, put his finger on one of the entries, and wrote down the corresponding character from a 27-symbol ‘alphabet’ (26 letters, plus a space):
XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD.
Each character was chosen randomly and independently, with no letter exerting a ‘pull’ on any other. This is the printed equivalent of static – what Shannon called ‘zero-order approximation’.
But, of course, we don’t choose our letters with equal probability. About 12 per cent of English text is comprised of the letter ‘E’, and just 1 per cent of the letter ‘Q’. Using a chart of letter frequencies that he had relied on in his cryptography days, Shannon recalibrated the odds for every character, so that 12 per cent of entries in the random-number book, for instance, would indicate an ‘E’. Beginning again with these more realistic odds, he arrived at what he called ‘first-order approximation’:
OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL.
We also know that some two-letter combinations, called ‘bigrams’, are much likelier than others: ‘K’ is common after ‘C’, but almost impossible after ‘T’; a ‘Q’ demands a ‘U’. Shannon had tables of these two-letter ‘bigram’ frequencies, but rather than repeat the cumbersome process, he took a cruder tack. To construct a text with reasonable bigram frequencies, ‘one opens a book at random and selects a letter at random on the page. This letter is recorded. The book is then opened to another page and one reads until this [first] letter is encountered [again]. The succeeding letter is then recorded. Turning to another page this second letter is searched for and the succeeding letter is recorded, etc.’
Just as letters exert ‘pull’ on nearby letters, words exert ‘pull’ on nearby words
Shannon didn’t specify the book he used, but any non-technical book in English should offer roughly similar results. If all goes well, the text that results reflects the odds with which one character follows another in English. This is ‘second-order approximation’:
ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TUCOOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE.
Out of nothing, a probabilistic process has blindly created five English words (‘on’, ‘are’, ‘be’, ‘at’, and, at a stretch, ‘Andy’).
‘Third-order approximation’, using the same method to search for trigrams, brings us even closer to passable English:
IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONSTURES OF THE REPTAGIN IS REGOACTIONA OF CRE.
You can do the same thing with the words themselves. From the perspective of information theory, words are simply strings of characters that are more likely to occur together. Here is ‘first-order word approximation’, in which Shannon chose whole words based on their frequency in printed English:
REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD BE THESE.
But just as letters exert ‘pull’ on nearby letters, words exert ‘pull’ on nearby words. Finally, then, Shannon turned to ‘second-order word approximation’, choosing a random word, flipping forward in his book until he found another instance, and then recording the word that appeared next:
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.
Comparing the beginning of the experiment with its end – ‘XFOML RXKHRJFFJUJ’ versus ‘ATTACK ON AN ENGLISH WRITER’ – sheds some light on the difference between the technical and colloquial significance of ‘information’. We might be tempted to say that ‘ATTACK ON AN ENGLISH WRITER’ is the more informative of the two phrases. But it would be better to call it more meaningful. In fact, it is meaningful to English speakers precisely because each character is less surprising, that is, it carries less (Shannon) information. In ‘XFOML RXKHRJFFJUJ’, on the other hand, each character has been chosen in a way that is unconstrained by frequency rules; it has been chosen from a 27-character set with the fairest possible odds. The choice of each character resembles the flip of a (27-sided) fair coin. It is analogous to the point at the top of Shannon’s parabolic graph, in which information is at a peak because the uncertainty of the outcome is maximised.
What does any of this have to do with the internet, or with any kind of system for transmitting information? That question brings us to Shannon’s second key insight: we can take advantage of messages’ redundancy. Because the symbols in real-world messages are more predictable, many don’t convey new information or surprise. They are exactly where we expect them to be, given our familiarity with ‘words, idioms, clichés and grammar’. Letters can be harmlessly excised from written English, for example: ‘MST PPL HV LTTL DFFCLTY N RDNG THS SNTNC’, as Shannon aptly noted. Words can also be redundant: in Shannon’s favourite boyhood story, Edgar Allan Poe’s ‘The Gold-Bug’ (1843), a treasure hunter takes advantage of repeated strings of characters to crack a pirate’s coded message and uncover a buried hoard.
Shannon expanded this point by turning to a pulpy Raymond Chandler detective story, ‘Pickup on Noon Street’, in a subsequent paper in 1951. Just as the rules of spelling and grammar add redundancies to human languages, so too can the vague but pervasive expectations of context. He flipped to a random passage in Chandler’s story, which he then read out letter by letter to his wife, Betty. Her role was to guess each subsequent letter until she got the letter right, at which point Shannon moved on to the next one. Hard as this was at the beginning of words, and especially at the beginning of sentences, Betty’s job grew progressively easier as context accumulated. For instance, by the time they arrived at ‘A S-M-A-L-L O-B-L-O-N-G R-E-A-D-I-N-G L-A-M-P O-N T-H-E D’, she could guess the next three letters with perfect accuracy: E-S-K.
To write is to write ourselves into a corner: up to 75 per cent of written English text is redundant
Betty’s correct guess tells us three things. First, we can be fairly certain that the letters E-S-K add no new information to the sentence; in this particular context, they are simply a formality. Second, a phrase beginning ‘a small oblong reading lamp on the’ is very likely to be followed by one of two letters: D, or Betty’s first guess, T (presumably for ‘table’). In a zero-redundancy language using our alphabet, Betty would have had only a 1-in-26 chance of guessing correctly; in our language, by contrast, her odds were closer to 1-in-2. Third, the sentence’s predictability goes even further: out of the hundreds of thousands of words in a typical English dictionary, just two candidates were extremely likely to conclude the phrase: ‘desk’ and ‘table’. There was nothing special about that phrase: it was an ordinary phrase from a random page in a random paperback. It showed, though, that to write is almost always to write ourselves into a corner. All in all, Shannon speculated that up to 75 per cent of written English text is redundant.
The predictability of our messages is fat to be cut – and since Shannon, our signals have travelled light. He didn’t invent the idea of redundancy. But he showed that consciously manipulating it is the key to both compressing messages and sending them with perfect accuracy. Compressing messages is simply the act of removing redundancy, leaving in place the minimum number of symbols required to preserve the message’s essence. We do so informally all the time: when we write shorthand, when we assign nicknames, when we invent jargon to compress a mass of meaning (‘the left-hand side of the boat when you’re facing the front’) into a single point (‘port’).
But Shannon paved the way to do this rigorously, by encoding our messages in a series of digital bits, each one represented by a 0 or 1. He showed that the speed with which we send messages depends not just on the kind of communication channel we use, but on the skill with which we encode our messages in bits. Moreover, he pointed the way toward some of those codes: those that take advantage of the probabilistic nature of information to represent the most common characters or symbols with the smallest number of bits. If we could not compress our messages, a single audio file would take hours to download, streaming videos would be impossibly slow, and hours of television would demand a bookshelf of tapes, not a small box of discs. All of this communication – faster, cheaper, more voluminous – rests on Shannon’s realisation of our predictability.
The converse of that process, in turn, is what protects our messages from errors in transmission. Shannon showed that we can overcome noise by rethinking our messages: specifically, by adding redundancy. The key to perfect accuracy – to be precise, an ‘arbitrarily small’ rate of error, as he put it – lies not in how loudly we shout down the line, but in how carefully we say what we say.
Here’s a simple example of how it works (for which we’re indebted to the science historian Erico Marui Guizzo). If we want to send messages in a four-letter alphabet, we might start by trying the laziest possible code, assigning each letter two bits:
A = 00
B = 01
C = 10
D = 11
But noise in our communication system – whether through a burst of static, interference from the atmosphere, or physical damage to the channel – can falsify bits, turning a 0 into a 1. If just one of the bits representing C ‘flipped’, C would vanish somewhere between sender and receiver: it would emerge as B or D, with the receiver none the wiser. It would take just two such flips to turn ‘DAD’ to ‘CAB’.
Ordinary languages, though, happen to be very good at solving this problem. If you read ‘endividual’, you recognise it as a kind of transmission error – a typo – and not an entirely new word. Shannon showed that we can import this error-proofing feature from language into digital codes, strategically adding bits. In the case of the four-letter language, we could use a code like this:
A = 00000
B = 00111
C = 11100
D = 11011
Now any letter could sustain damage to any one bit and still resemble itself more than any other letter. It takes fully three errors to turn one letter into another. Our new code resists noise in a way our first one did not, and we were not forced to pump any more power into our medium of communication. As long as we respect the inherent ‘speed limit’ of the communication channel (a limit in bits per second that Shannon also defined) there is no limit on our accuracy, no degree of noise through which we cannot make ourselves heard. Shannon had not discovered the precise codes for doing so in practice – or the ways to combine codes that compress and codes that were error-proof – but he proved that such codes must exist.
Shannon’s work is the reason these words are appearing on your screen
And so they did. In the long-horizon spirit of Bell Labs, the codes would take decades to develop, and indeed, the questions posed by Shannon remain objects of study for engineers and information theorists to this day. Nevertheless, Shannon had shown that by converting any message – audio, visual, or textual – into digital bits, we could communicate anything of any complexity to anyone at any distance. His work is the reason these words are appearing on your screen.
Though it was marked by intellectual freedom and scientific celebrity, Shannon’s life did end with an acute unfairness. As the digital world he inaugurated began to flourish in the 1990s, Shannon was slipping into Alzheimer’s disease. His awareness of the practical payoff of his work was severely and tragically limited. But as to the ambition and sheer surprise of the work itself, no one put it better than his colleague John Pierce: ‘it came as a bomb’.
The source of that power lay in Shannon’s eagerness to explore information’s deep structure. In his hands, it became much more than a mechanical problem of moving messages from place to place; it began with rethinking what it means to communicate and to inform, in the classical sense. It was an old question – but now we live in an age of information, in large part, because of how Shannon gave that old question new life.






