The Middle Ages still suffers from the embarrassment of comparison. Before it glowed the light of the ancient Greeks – the great, early speculators of the natural world and our place in it. After the Middle Ages came the scientific revolution – Copernicus, Galileo, Newton – and the surging onrush of modernity. Even if the idea of the so-called ‘dark ages’ is waning, there remains the widespread impression that the Middle Ages is in some sense a time of stagnancy, especially in its understanding of science and the natural world. Is this an accurate view of medieval science? There is one discipline, often overlooked, that serves to illuminate the Middle Ages, as well as its place in the history of scientific thought: mechanics.
The predominant assumption about the rise of modern science is that it went hand in hand with the conception of nature as a universal mechanism. By viewing nature in this way, it could be studied, analysed and experimented upon with mathematical rigour, and its functioning could be elucidated by physicists harnessing empirical methods. While the motion of inanimate bodies became theorised on the model of projectiles, some mechanical philosophers even claimed that the complex organisation of animate bodies could be understood on the model of levers, springs, pulleys and other mechanical devices. This step – nature as a universal mechanism – is often seen as the important break from the Middle Ages.
But, in fact, mechanics was not unknown in the Middle Ages, and medieval thinkers continuously discussed mechanical problems at the crossroads of natural philosophy and mathematics. Mechanics enjoyed continuous interest and progress throughout the Middle Ages, and modern physicists and mathematicians relied to a large extent on results inherited from the Middle Ages. But mechanics as a scientific discipline did not always go under that name.
Taking this into account, a close look at the Middle Ages reveals that the consideration of mechanics as a core part of physics, together with the mathematical treatment of weights, forces and resistances, all generally assumed to characterise the birth of modern science, was there long before Galileo. That means that medieval thinkers did not simply lay the foundations of the scientific revolution. It means they started it. There should be no more embarrassment of comparison for that great era of scientific thought, especially when we review the fascinating history of mechanics.
For the Greeks, mēkhanikē (μηχανική) meant the science ‘of machines’, or ‘of devices’, that can produce motions against nature, which means a motion contrary to the internal inclination of natural bodies. A stone, being a heavy body, is internally inclined to move downward, whereas a fire, being a light body, is internally inclined to move upward. Machines are technological devices that make it possible to go against this natural tendency: the pulley, for example, enables one to lift a heavy body, despite the fact that it’s inclined to move downward.
The status attributed to a discipline, whether it is an art, a practice or a true science, is crucial for understanding how it was conceived. It shows how philosophers and scientists defined the discipline’s role and scope but it also reflects, because of that, how they regarded nature and the Universe. The science of devices was conceived by Greek scientists as a discipline in between physics (or natural philosophy) and mathematics. Aristotle granted a special status to theoretical disciplines that partake in both physics and mathematics, such as astronomy, music and optics. He attributed a similar status to mechanics.
Hero also invented a mechanical vending machine that, reportedly, sold holy water to the faithful
The Mechanical Problems (Problemata mechanica) – one of the first treatises dealing with simple tools and mechanical devices, long attributed to Aristotle, and destined to achieve great popularity in the Renaissance – was composed in the early Aristotelian school. But it wasn’t until the Hellenistic thinkers of the city of Alexandria that the most significant developments of Greek mechanics took place. The theoretical study of forces and resistances proper to bodies (rigid or liquid) was for them intimately bound up in the engineering of innovative machines.
Archimedes, the best-known among these thinkers (though he lived in Alexandria only briefly), invented several ingenious devices, such as systems of compound pulleys able to lift heavy objects that were impossible to move with simple pulleys. He also helped lay the scientific bases of mechanics, explaining, for instance, the functioning of the water screw (which makes it possible to pump water from rivers) and providing a mathematical demonstration of the law of the lever (the law about a balancing beam with different weights along its length). However, the most creative inventor of the time was Hero of Alexandria (1st century CE). Besides describing one of the first steam-powered turbines (the so-called ‘aeolipile’), Hero remains famous for having conceived an ‘automatic theatre’: a fully automatic puppet show representing an episode from Greek mythology. He also invented a mechanical vending machine that, reportedly, sold holy water to the faithful.
For these ancient scientists, such amusing inventions were only the fun part of a much more serious project: the construction of a true science involving fundamental physics and mathematics. The hybrid character of mechanics was indeed already present in these early developments of Greek philosophers and scientists. While the Mechanical Problems was mainly based on a theory of velocities and forces, the works belonging to the Archimedean tradition showed a more mathematical approach in which central theorems like the law of the lever were based on geometrical demonstrations, without appealing to the physical notion of force, strictly speaking.
The shift from Greek to Latin as the primary scientific language in the western Roman Empire made Greek sources less accessible in Europe. The eventual collapse of the empire meant that science and philosophy came to a standstill in Latin Europe, so the next chapter of the story of mechanics took place when, with the expansion of Islamic culture, Greek philosophy was recollected and integrated in the Arabic-speaking world. When the treasures of Greek science and philosophy had been transmitted to the Arabic world, the ‘science of machines’ enjoyed a second life enriched with new developments. What really changed was, however, the name and definition of that discipline.
In Arabic treatises on the topic, the science of machines or devices was distinguished from the science of weights. Whereas the former dealt with simple machines (ḥiyal) like the lever, the inclined plane, the screw or the pulley, the latter was concerned with the concepts of equilibrium and weights, and therefore made an essential use of the balance (mīzān). This special focus on the balance and properties related to weights, forces and velocities led to a detachment of the investigation of their different relations from the more practical purposes related to the study of machines and their usefulness for practical matters.
Significant writings on simple machines were composed in the Arabic tradition by many philosophers and scientists like the Banū Mūsā brothers in the 9th century. In their Book of Tricks (Kitāb al-Ḥiyal), they presented an impressive list of mechanical devices, some of which were improvements from ancient Greek machines, while others were of their own invention, like hydraulic regulation devices, ventilation systems, lamps that automatically switched off, and even programmable musical instruments. Less pleasant, yet historically important, practical applications of the science of weights in the Arabic world included the counterweight trebuchet described by Mardi ibn Ali al-Tarsusi, a 12th-century writer who studied military matters. But it was Thābit ibn Qurra in the 9th century who composed one of the most important treatises of medieval mechanics dealing mainly with balance and weights, the Kitāb fi al-Qarastūn, which would become known in the Latin West as the Liber Karastonis.
Jordanus articulated and merged what we nowadays call ‘statics’ with a physical theory on the causes of motion
A major event in Western intellectual history was the translation from the 12th century onward of ancient scientific and philosophical sources into Latin. Besides the most influential Greek writings of Aristotle, many new works came to the Latin world from Arabic. The transmission of Arabic texts in the Latin West reinforced the scientific character of investigations concerned with mechanics. The classification of theoretical disciplines due to Dominicus Gundissalinus in the 12th century, inspired by Al-Fārābī’s characterisation of sciences, defined the science of weights (scientia de ponderibus) as a theoretical discipline and as a mixed science, a definition that would turn out to be crucial for the later development of this discipline.
The science of weights received considerable developments in the Latin tradition. Its most important contributor was a certain Jordanus de Nemore, of whom we still know little. His writings, composed in the 13th century, achieved a remarkable synthesis of the different traditions of mechanics dealing with simple machines and weights. In line with the Arabic tradition of the science of weights, Jordanus’s method takes the balance as the fundamental instrument from which the law of the lever and, from the law of the lever, the laws governing all other simple machines may be deduced. But the most remarkable aspect of Jordanus’s treatises on weights lies in the fact that he managed to ground the mathematical results of the Archimedean approach, based on the use of geometry for understanding equilibria, with the dynamic approach proper to the Aristotelian tradition that drew on the concepts of velocities and forces and, consequently, was more interested in the physical causes of motions. In this way, Jordanus managed to finely articulate and merge what we would nowadays call ‘statics’ with a physical theory on the causes of motion (closer to what we could anachronistically call ‘dynamics’).
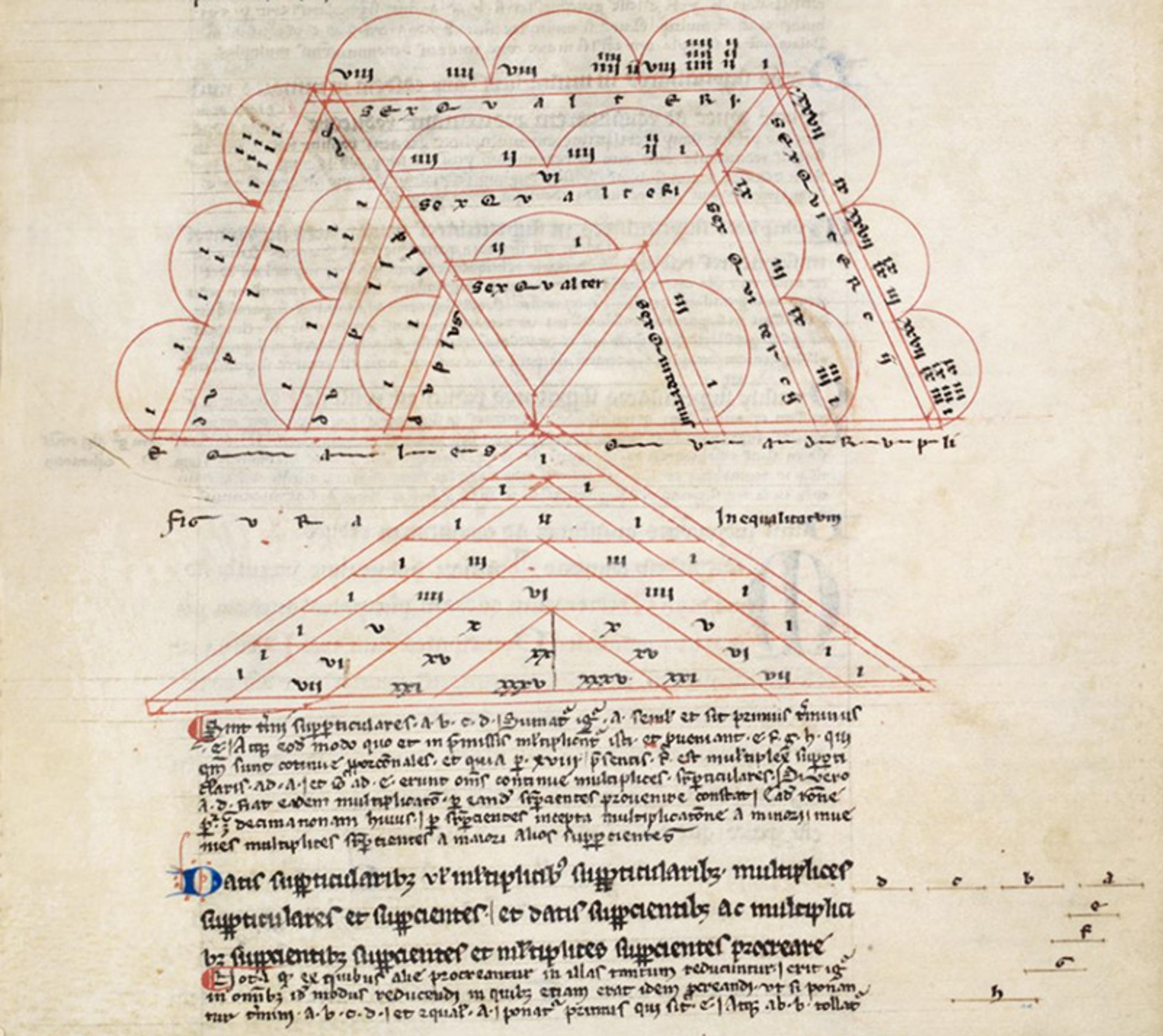
From De elementis arithmetice artis by Jordanus de Nemore, 13th century. Harley MS 4973. Courtesy the British Library
Jordanus’s writings were quoted by many eminent philosophers who contributed to the rise of a new physics in the 14th century onward, like Thomas Bradwardine, Nicole Oresme, Albert of Saxony and John Dumbleton. These authors were interested in possible applications of the science of weights, including hydrostatics and aerostatics (the branches of mechanics studying liquids and gas in equilibrium, in modern terms), to the making of new technological devices. The 13th-century philosopher Roger Bacon was particularly visionary. In his Letter Concerning the Marvellous Power of Art and of Nature, and Concerning the Nullity of Magic, he imagines wonderful machines such as automatically driven boats, submarines and suspension bridges. These were not the only possible technologies discussed by medieval thinkers in light of the science of weights. Although he did not know the real composition of the atmosphere, Albert of Saxony conceived of a machine structurally similar to a hot-air balloon some 400 years before humans would make these a reality.
It is usually claimed that the new interest for mechanics rose in the 16th century with the first editions and translations of the Mechanical Problems. It is indeed undeniable that the availability of this text stimulated new developments on the theoretical level and new inventions on the practical level, just as it is true that a more experimental conception of scientific knowledge emerged in the 16th century. However, the results and degree of technicality of the Mechanical Problems were far inferior to Jordanus’s works, which were still extensively used and quoted by 16th-century scientists and philosophers.
Many ideas that became associated with modern physics can be found already in Jordanus’s treatises. Let us take, for instance, the principle of component motions, ie the idea that the visible motion of a body, even having a complex trajectory and great variation of speed, can always be analysed as resulting from different, more basic motions composing it. This principle and the corollary view that motions can be analysed as the visible effect of a composition of forces were present in this work long before the works of Galileo and other founders of modern physics. It is no surprise that one of the first systematic treatises on cannonballs – analysing the trajectory of projectiles by decomposing their motion – was written in 1537 by Niccolò Tartaglia, a mathematician well versed in the medieval science of weights. So, while the Mechanical Problems was an exciting intellectual event, it by no means revolutionised the study of mechanics. It is to the medieval tradition and Jordanus’s works we should look for the foundations of modern mechanics.
The Latin works of Jordanus, and other related writings, are not an isolated event of Western intellectual history. As Joel Kaye has suggested in A History of Balance, 1250-1375 (2014), the interest in balances, equilibria and weights – as well as the use of mathematics for analysing physical processes – accompanied a more global change of paradigm. Other indications of this nascent revolution can be found in the will to quantify natural phenomena, the monetisation of Europe and, most relevant for our topic, the invention of mechanical clocks in Europe at the end of the 13th century. These historical events converged from different angles to the same idea: that things can be measured. Whether the interest of Latin thinkers for the study of scales and weights should be viewed as one of the causes of these cultural changes or, rather, as one of the effects that resulted from them is a matter of dispute. But it can hardly be denied that it played an important role in the growing tendency to introduce mathematical considerations into the study of natural processes.
The initial understanding of mechanics was that of a practical discipline that serves human interests
As just stated, the new translation of the Mechanical Problems at the dawn of the modern period did not radically change the way people conceived of mechanics as a scientific discipline. What really changed was the word, not the thing. The recovery of the Mechanical Problems enabled 16th-century thinkers to realise what was the real nature of the science that Aristotle had called ‘mechanics’ in some of his works. Despite the massive number of commentaries devoted to Aristotle in the prior centuries, medieval thinkers could only speculate about the exact reference of the term ‘mechanics’ that they found here and there in Aristotle’s writings, and did not realise that it corresponded with what they had been calling ‘science of weights’. In the Latin tradition, the term ‘mechanics’ had been most often associated with the mechanical arts, as opposed to the (seven) liberal arts – astronomy, mathematics, geometry, music, rhetoric, grammar, and dialectic or logic. By contrast with these fine arts, the mechanical arts referred to a wide variety of practices including architecture, agriculture, pottery, weaving and similar crafts that were classified as ‘arts’ in the sense of practical disciplines whose aim was not the pure study of nature proper to theoretical science but the concrete production of goods for human benefits.
The status of a mixed theoretical science granted to the science of weights had at least three important consequences. First, the science of weights could be theorised on the same level as other theoretical disciplines, although its proper mode of demonstration – in between that of natural philosophy and that of mathematics – had to be elucidated. Philosophers came to claim that the science of weights could be considered a deductive science provided that one and the same science may contain terms belonging to different scientific fields (natural philosophy and mathematics).
Second, scientific status had very significant consequences for the medieval conception of knowledge and the type of scientific discourse allowed in this conception. In the Middle Ages, it was Aristotle’s theory of science that determined the way philosophers classified and circumscribed fields of knowledge. According to a principle of Aristotle’s philosophy, there exist fundamental categories of being that cannot be predicated of one another. A colour does not exist in the same way as a number, a moment or a place, just like a horse does not exist in the same sense as a quality like heat exists. This led Aristotle to conceive a sophisticated theory of science in which different types (‘genera’ in Aristotle’s technical words) of beings had to be either studied separately or related to one another according to precise rules.
In the resulting classification of sciences, mathematics was, for instance, conceived as a science dealing essentially with quantity. But for this reason, Aristotle’s theory of science left little room for mathematical physics, which implies the possibility of predicating quantitative attributes (like numbers) to non-quantitative entities (like qualities and substances). The Latin tradition of the science of weights, understood a theoretical but mixed science in between physics and mathematics, implied applying mathematical concepts to physical phenomena. The tradition of Arabic and, from the 13th century onward, Latin mechanics played a role in the application of mathematics to physics, which is central to modern science.
Third, the division of mechanics into a science of devices and a science of weights, the latter being taken up by Latin scientists, was instrumental in the gradual identification of the subject of mechanics with the laws of nature themselves. The aim of the Greek mēkhanikē was to study the production of motions against nature due to machines. So the initial understanding of mechanics was that of a practical discipline that serves human interests, and not of a theoretical discipline that studies the laws of nature independently from a practical perspective. The redefinition of mechanics as a science of weights consequently led to merging this discipline in the broader scope of natural philosophy, conceived as a theoretical discipline, and gradually identifying its object with the laws of nature themselves.
In light of these observations, the long-told story about the replacement of the old Aristotelian philosophy of nature due to the rise of mechanics in the 17th century and about the true novelty of modern mechanics is nothing but a myth. Long before the introduction of the Mechanical Problems as part of the official teaching for masters holding the Chair of Mathematics at the University of Padua in the second half of the 16th century, philosophers did not hesitate to include works of mechanics or the science of weights in writings devoted to expounding Aristotle’s natural philosophy.
At the end of the 14th century, Blasius of Parma, a master at the University of Padua, discussed several problems connected to the science of weights in his Questions on Physics. Blasius of Parma incorporates theorems of statics (demonstrated through the properties of balances) and hydrostatics (the branch of mechanics dealing with fluids) within the context of Aristotelian physics, seeking to accommodate this knowledge with a rigorous analysis of the notions of heaviness and lightness. Just like the 14th-century philosophers Bradwardine, Oresme and Albert of Saxony before him – and many others after him – Blasius was willing to integrate into the physical theories of his time the results of a long, continuing tradition of mechanics that he regarded as indisputable.
John of Holywood had designated the Universe created by God as the ‘machine of the world’
So, when the Mechanical Problems was received in the Latin West, the scientific status of mechanics as well as the theoretical integration of this discipline in the broader framework of natural sciences were, to a large extent, already endorsed. The pivotal role of instruments designed and theorised in the Middle Ages, such as the balance, was still acknowledged in the late 16th century by Galileo, who was well acquainted with the Mechanical Problems, as his position of professor of mathematics in Padua required:
We, desiring now to discuss this matter, in order to proceed in an orderly way, shall begin by considering the nature of the first and simpler machines, to which the other reduce or from which they are compounded. These simple machines are five in number: the lever, the capstan, the pulley, the screw, and the stamp or force of impact. All of these again reduce in a certain way to a single one, that is to the balance.
– from Delle machine (c1593) by Galileo, translated by W R Laird
From these historical facts, it will appear more clearly why and how the modern identification took place – explicitly stated by Galileo, Francis Bacon and René Descartes – of nature with a type of mechanism whose secrets must be investigated by the natural philosopher. The invention of mechanical clocks which, unlike most previous human inventions, did not require anything to keep moving once set in motion, had already modified the way philosophers conceived of nature with respect to machines. In the 14th century, Oresme compared the world to a clock, an analogy later taken up by Kepler in the 17th century. As early as the first half of the 13th century, John of Holywood had designated the Universe created by God as the ‘machine of the world’ (machina mundi). This expression, later quoted by Robert Grosseteste, Giovanni Pico della Mirandola, Nicholas of Cusa and Copernicus, was well known to the 16th-century commentators of the Mechanical Problems, including Galileo, who quotes John of Holywood in his lectures given in Padua. But while the expression could still be regarded as a mere metaphor in the earlier Middle Ages, it had acquired a much more literal meaning by the time modern thinkers undertook to explain nature according to a mechanistic model. The development of medieval mechanics, the redefinition of its scope and acquisition of a new status were key to this evolution.

From Sphaera Mundi published 1485. Courtesy the Met Museum, New York
The central importance of mechanics for modern science did not come from nowhere. Recent converging studies allow to affirm that, during the Middle Ages, especially in the Arabic and in the Latin worlds, major advances ensured the transmission of a long, rich and persisting tradition of mechanics to modern philosophers and scientists. What is more, the redefinition of mechanics and its scope paved the way in many respects for the modern identification of the subject of natural philosophy with the laws studied by mechanics.
For a long time, people in the Middle Ages did not really know that they were investigating mechanics to the extent that they did not possess the original word for it. Precisely because of that, the science they conceived became a full part of physics conceived as the study of nature and its laws, rather than a mere craft aimed at serving human interests. This fact not only confirms how much the history of knowledge is indebted to the Middle Ages, especially where modernity proudly claimed to have got rid of what medievals had produced. It raises important questions as to the names and categories we use for understanding the history of knowledge and, so, for determining where and when science and philosophy existed. It also reminds us of an important lesson about the advancement of learning as such: that it is perfectly possible to do important science without knowing it.