Imagine throwing a baseball and not being able to tell exactly where it’ll go, despite your ability to throw accurately. Say that you are able to predict only that it will end up, with equal probability, in the mitt of one of five catchers. The baseball randomly materialises in one catcher’s mitt, while the others come up empty. And before it’s caught, you cannot talk of the baseball being real – for it has no deterministic trajectory from thrower to catcher. Until it becomes ‘real’, the ball can potentially appear in any one of the five mitts. This might seem bizarre, but the subatomic world studied by quantum physicists behaves in this counterintuitive way.
Microscopic particles, governed by the laws of quantum mechanics, throw up some of the biggest questions about the nature of our underlying reality. Do we live in a universe that is deterministic – or given to chance and the rolls of dice? Does reality at the smallest scales of nature exist independent of observers or observations – or is reality created upon observation? And are there ‘spooky actions at a distance’, Albert Einstein’s phrase for how one particle can influence another particle instantaneously, even if the two particles are miles apart.
As profound as these questions are, they can be asked and understood – if not yet satisfactorily answered – by looking at modern variations of a simple experiment that began as a study of the nature of light more than 200 years ago. It’s called the double-slit experiment, and its findings course through the veins of experimental quantum physics. The American physicist Richard Feynman in 1965 said that this experiment ‘has in it the heart of quantum mechanics’. Werner Heisenberg, the German physicist and founding member of quantum physics, would often refer to this strange experiment in his discussions with others to ‘concentrate the poison of the paradox’ thrown up by nature at the smallest scales.
In its simplest form, the experiment involves sending individual particles such as photons or electrons, one at a time, through two openings or slits cut into an otherwise opaque barrier. The particle lands on an observation screen on the other side of the barrier. If you look to see which slit the particle goes through (our intuition, honed by living in the world we do, says it must go through one or the other), the particle behaves like, well, a particle, and takes one of the two possible paths. But if one merely monitors the particle landing on the screen after its journey through the slits, the photon or electron seems to behave like a wave, ostensibly going through both slits at once.
When microscopic entities have the option of doing many things at once – like that metaphysical baseball – they seem to indulge in all possibilities. Such behaviour is impossible to visualise. Common sense fails us when dealing with the world of the quantum. To explain the outcome of something as simple as a particle encountering two slits, quantum physics falls back on mathematical equations. But unlike in classical physics, where the equations let us calculate, say, the precise trajectory of a baseball, the equations of quantum physics allow us to make only probabilistic statements about what will happen to the photon or electron. Crucially, these equations paint no clear picture about what is actually happening to the particles between the source and the screen.
It’s no wonder then that different interpretations of the double-slit experiment offer alternative perspectives on reality. For example, in the late 1920s and early ’30s, some physicists made the startling claim that a particle going through two slits has no clear path or indeed no objective reality until one observes it on a screen on the other side. At a gathering of physicists and philosophers at the Carlsberg mansion near Copenhagen in 1936, the Dutch physicist Hendrik Casimir recalled someone protesting: ‘But the electron must be somewhere on its road from source to observation screen.’ To which Niels Bohr, one of the founders of quantum mechanics, replied that the answer depends on the meaning of the phrase ‘to be’. In other words, what does it mean to say that something exists? One philosopher in the group that day, the Danish logical positivist Jørgen Jørgensen, retorted in exasperation: ‘One can, damn it, not reduce the whole of philosophy to a screen with two holes.’
Yet it is extraordinary just how much of quantum physics and philosophy can be understood using a screen with two holes – or variations thereof. The history of the double-slit experiment goes back to the early 1800s, when physicists were debating the nature of light. Does light behave like a wave or is it made of particles? The latter view had been advocated in the 17th century by no less a physicist than Isaac Newton. Light, Newton said, is corpuscular, or constituted of particles. The Dutch scientist Christiaan Huygens argued otherwise. Light, he said, is a wave – the name given to the vibrations of the medium in which the wave is travelling. For example, a wave in water is essentially the way water moves up and down as the wave propagates. Huygens argued that light is vibrations in an all-pervading ether.
In the first years of the 19th century, the English polymath Thomas Young seemingly settled the debate. He was the first to perform an experiment with a ray of sunlight, a sunbeam, through two narrow slits. On a screen on the other side, he observed not two strips of light – as you’d expect if light is made of particles going through one slit or the other – but a pattern of alternating bright and dark fringes, characteristic of two sets of waves interacting with each other.
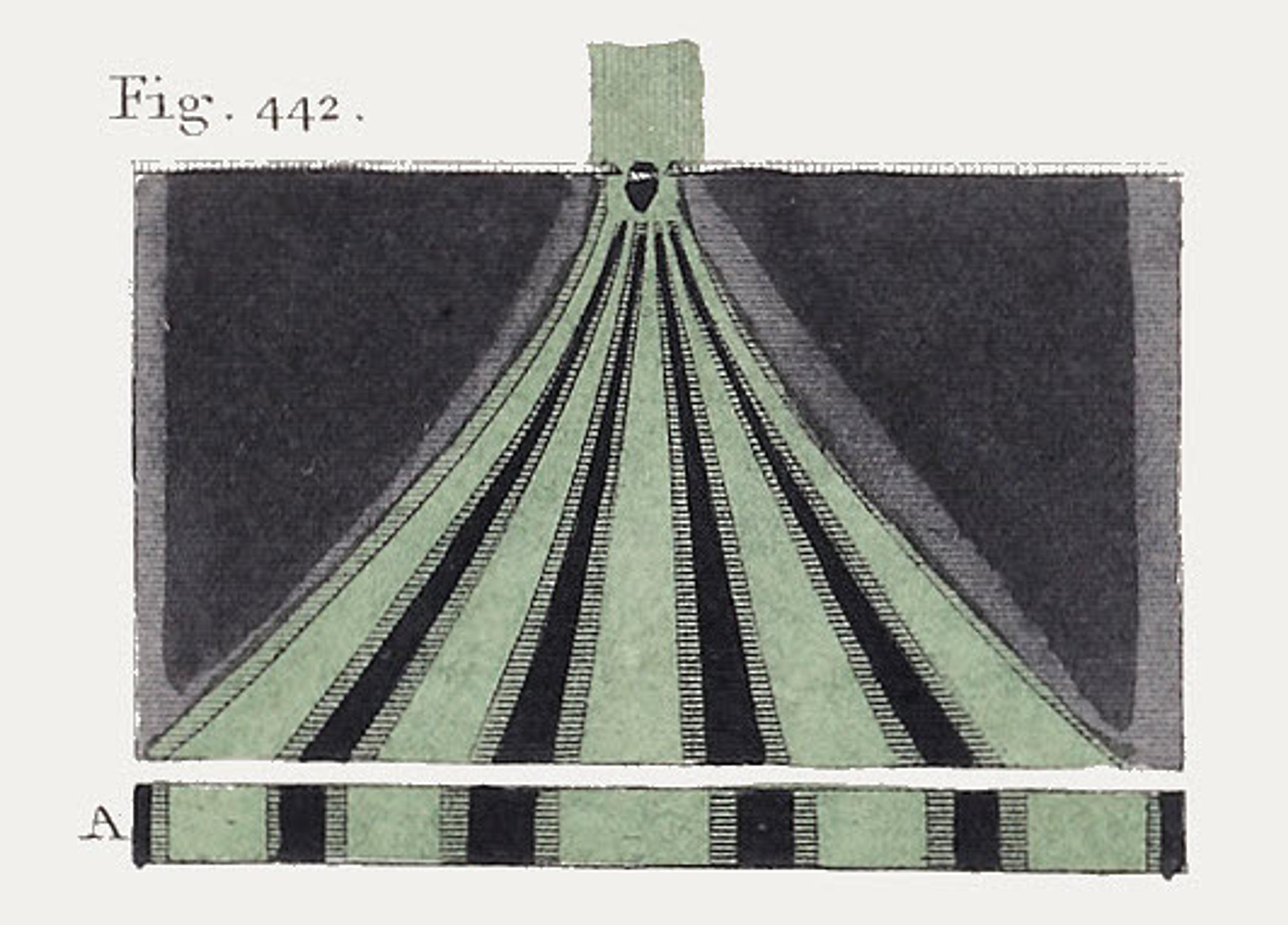
Fig 442 from Thomas Young’s ‘Lectures’ published in 1807 detailing his original ‘two-slit’ experiment. Courtesy Wikimedia.
Imagine an ocean wave hitting a coastal breakwall that has two openings. New waves spread out from each opening and head toward the coast. These waves eventually overlap and interfere – at some places constructively (where the crest of one wave meets the crest of another), and at some places destructively (the crest of one wave encounters the trough of another). In Young’s experiment, he saw similar interference. The fringes that he observed had bright regions indicative of constructive interference and dark regions typical of destructive interference.
This view of light as a wave gained strong mathematical support when the Scottish physicist James Clerk Maxwell developed his theory of electromagnetism in the 1860s, showing that light, too, is an electromagnetic wave.
That would have been the end of story – if not for the birth of quantum physics, which began with the German physicist Max Planck’s argument in 1900 that energy comes in quanta, or tiny, indivisible units. Then, in 1905, Einstein studied the photoelectric effect, in which light falling on certain metals dislodges electrons; the effect can be explained only if light is also made of quanta, with each quantum of light analogous to a particle. These quanta of light came to be called photons.
Now, the double-slit experiment gets maddeningly counterintuitive.
Imagine beaming light at two slits one quantum, or particle, at a time. Our classical sensibilities tell us that the photon has to go through one slit or the other. And on the screen on the other side (say, a photographic plate that records photons as they arrive one by one), each photon creates a spot, and we expect these spots to pile up behind the two slits and form two bright strips.
But it’s the quantum world, so of course that’s not what happens.
As the photons land on the photographic plate, over time an interference pattern emerges. Each photon goes only to certain places on the plate – to regions that would represent constructive interference if light were a wave. The photons mostly avoid regions that represent destructive interference. It’s a clear sign of interference and wave-like behaviour.
But our source is emitting light one photon at a time. The photographic plate is recording its arrival as an individual particle. And – this is crucial – the photons are going through the apparatus one at a time. There’s no interaction between one photon and the next, or the first photon and the 10th, and so on. So, what’s interfering with what?
This is where the mathematics comes in. In the mid-1920s, a few fabulously talented physicists, among them Heisenberg, Pascual Jordan, Max Born and Paul Dirac in one group, and Erwin Schrödinger on his own, developed two ways of mathematically depicting the behaviour of the quantum underworld. These two ways turned out to be equivalent. It boils down to this: the state of any quantum system is represented by a mathematical abstraction called a wavefunction. There is a single equation – called the Schrödinger equation – which tells us how this wavefunction, and hence the state of the quantum system, changes with time. This is what allows physicists to predict the probabilities of experiment outcomes.
The wavefunction starts to spread, as a wave would, with different values at different places
In the context of the double-slit experiment, think of the wavefunction as an undulating surface that encodes information about the location of the photon. When the photon emerges from its source, the wavefunction is peaked at one location, and nearly zero everywhere else, suggesting that the photon is localised near the source.
But now mathematics kicks in. The progress of the photon can be captured by the Schrödinger equation, which reveals how the wavefunction evolves with time. The wavefunction starts to spread, as a wave would, with different values at different places. These values are related to the probabilities of finding the particle in those locations, should you choose to look.
As this wavefunction spreads, it encounters the two slits. And just like a wave of water hitting two openings in the breakwall, the wavefunction (which, don’t forget, is a mathematical abstraction) splits: one component goes through the left slit and the other through the right slit. Two wavefunctions emerge from the other side, and each spreads and evolves, still according to the Schrödinger equation. All this is deterministic and predictable. By the time the individual wavefunctions reach the photographic plate, they have spread out enough to start interfering with each other like the waves in the ocean. The photon’s state is now given by a wavefunction that is a combination of the two components’ interfering wavefunctions: the photon itself is now said to be in a ‘superposition’ of having gone through both slits. At the photographic plate, upon detection, this combined wavefunction again peaks in one location and goes to more or less zero everywhere else. The photon is registered at that location.
It all seems to make sense – sort of – until you start digging into the mathematical equations. What’s a wavefunction and what does it mean for a wavefunction to go through two slits? Is the wavefunction something real? And how does one figure out where the wavefunction will peak when it encounters the photographic plate? Why does it peak there and not elsewhere?
In the equations of quantum mechanics, the wavefunction is, well, a mathematical function. For any quantum system with more than two particles, the wavefunction does not live in the three familiar spatial dimensions of our world. Rather, it exists in something called a configuration space (an abstract mathematical space, the number of dimensions of which mushrooms with increasing number of particles, but we can ignore that for now).
In the summer of 1926, just months after Schrödinger came up with his eponymous equation for the evolution of the wavefunction, Born figured out that the value of the wavefunction at a given point in space and time can be used to calculate the probability of, for example, finding the photon at that location. For the double slit, it turns out that the probabilities are very low for regions where the two components of the wavefunction interfere destructively, and high for regions where they interfere constructively.
All this seems tantalisingly understandable, but upon closer examination more questions appear. Did the photon go through both slits at once? Does the photon have a trajectory, as it leaves the source and is eventually detected at the photographic plate? And given that the mathematics says that there are many regions where the photon can be found with a non-zero probability, why does it end up in one of those regions and not others? Finally, if the photon didn’t go through both slits, but rather the wavefunction did, is the wavefunction real?
Trying to answer such questions takes us into the heart of what’s confounding about quantum mechanics, and brings us in contact with profound philosophical issues about the nature of reality.
Take the question of determinism. When you throw a baseball in the classical world, physics will tell you where it will land. Not so in the quantum realm. The wavefunction cannot predict the exact location at which the photon will land – only its probability of landing at any one of a number of spots. For any given photon, you can never predict with certainty where it will be found: all you can say is that it will be found in region A with probability X, or in region B with probability Y, and so on. These probabilities are born out when you do the experiment numerous times with identical photons, but the precise destiny of an individual photon is not for us to know. Nature at its most fundamental seems indeterminate, random.
The double-slit experiment also allows us to explore notions of realism, the idea that an objective reality exists independent of observers or observation. Recall Casimir’s account of the gathering at the Carlsberg mansion: common sense tells us that the photon must have a clear path from the source to the photographic plate. But the mathematical formalism of standard quantum mechanics does not have a variable that captures the position of a particle as it moves – only a starting point and an end point that is contingent upon observation. And so, the photon does not have a trajectory. In fact, in one way of interpreting the formalism – named the Copenhagen interpretation after the place where it took shape – the photon has no objective reality until it lands on the photographic plate. At its extreme, the Copenhagen interpretation is often said to be antirealist. More generally, antirealism takes the position that reality does not exist independent of an observer (an observer does not necessarily mean a conscious human, it could be a photographic plate; opinions vary on this).
Einstein was a realist. He was adamant that standard quantum mechanics is incomplete, in that it lacks the necessary variables to capture trajectory – the position and momentum of a particle as it moves. Einstein was also an avowed adherent of the principle of locality: the notion that something happening in one place cannot influence something happening elsewhere any faster than the speed of light. Taken together, this philosophical position is called local realism.
The opposite of locality – nonlocality – gets highlighted by something as simple as the double-slit experiment. When the photon’s wavefunction nears the photographic plate, the photon is in a quantum superposition of being in many places at once (this is not to say that the photon actually is in these places simultaneously, it’s just a way of talking about the mathematics; the photon itself is not yet ascribed reality in the standard way of thinking about it). Upon observation, the wavefunction is said to collapse, in that its value peaks at one location and goes to near-zero elsewhere. The photon is localised – and thus found to be at one of its many possible locations.
Surely a photon, which cannot be divided into further smaller parts, cannot go through both slits at once?
Einstein pointed out a problem with this scenario (he used a slightly different thought experiment than the double-slit, but the conceptual arguments are the same). If the wavefunction is something real – or is part of the ontology of the world, in the lingo of philosophers – then its collapse is a nonlocal event. A measurement caused the wavefunction to peak in one location and simultaneously go to zero elsewhere. In principle, the wavefunction could be spread across kilometres, and this scenario would still hold. Regions of spacetime far separated from each other would be instantly influenced by the measurement-induced collapse in one location.
There is another way to think about the wavefunction that avoids this difficultly. Many followers of standard quantum mechanics would say that the wavefunction is epistemic – it merely captures our knowledge about the reality. If so, the collapse is merely a sharpening of our knowledge about reality, and so it’s not a physical event and hence does not imply nonlocality.
But if the wavefunction is not real – then what goes through the two slits? Surely a photon, which cannot be divided any further into smaller parts, cannot go through both slits at once? Something must traverse both slits simultaneously to generate the interference pattern. If not the photon or its wavefunction, what else could it be? Epistemic or ontological, the questions about the wavefunction remain.
Besides the status of the wavefunction, perhaps the most well-known issue accentuated by the double-slit experiment is how something in the quantum realm can sometimes act like a wave and sometimes like a particle, a phenomenon called wave-particle duality. If we don’t care about knowing which slit a photon goes through, the photon behaves like a wave, and lands on a certain part of the photographic plate. When enough photons land on such parts, constructive interference fringes appear. Crucially, the photons almost never go to regions that will remain dark.
But our classical minds rebel. We cannot disregard the conviction that the photon has to go through one slit or the other. So we put detectors next to the slits (let’s assume that our detectors work without destroying the photons). Something weird happens. The photons will now go through one or the other slit. Curiously, this time they will not form an interference pattern. They act like particles and they will go to those regions on the photographic plate that they shunned when acting like a wave.
When Einstein and Bohr were arguing about the double-slit experiment, it was thought that the physical disturbance produced by the act of looking causes the interference pattern to disappear.
But since then, it’s become clear that the problem runs deeper. Experimentalists devised ways of determining which slit a photon goes through without, ostensibly, disturbing it. Turns out that the mere presence of this ‘which-way’ (welcher-weg in German) information in the environment – something that in principle can be extracted – destroys the interference pattern. The photons behave like particles.
Wave-particle duality was pushed to the extreme by ever more sophisticated versions of the double-slit experiment. In 1982, Marlan Scully, who was at the University of New Mexico, and Kai Drühl, of the Max Planck Institute for Quantum Optics in Munich, came up with one of the most memorable variations. What if there is a way to first collect information about which way a photon goes (causing it to act like a particle) and then erase this information? Would erasing the information cause the photons to act like waves – even after they presumably went through one slit or another as a particle and landed on the photographic plate?
The empirical answer to this famous quantum eraser question is an unequivocal yes. In 2000, Scully teamed up with Yoon-Ho Kim and colleagues at the University of Maryland in Baltimore and did this experiment using atoms that could be made to emit a pair of entangled photons (in mathematical terms, two entangled photons are described by the same wavefunction, so an action on one photon immediately influences the other, because of the collapse of the single wavefunction. Nonlocality is an explicit aspect of this version of the double-slit experiment). The experimental setup was engineered in such a way that if one photon of the entangled pair went through a double slit, the partner photon could be used to extract ‘which-way’ information about the first photon. Scully and colleagues showed that if you erased this information, the first photon acted like a wave; otherwise it acted like a particle.
It was clear that whether a photon behaves like a wave or a particle depends on the choice of the experimental setup. Based on this finding, in 1978 the American physicist John Wheeler dreamed up perhaps the most famous version of the double-slit experiment, which he called ‘delayed choice’.
Wheeler’s bright idea was to ask: what if we delayed the choice of the type of experiment to perform until after the photon had entered the apparatus? Say it enters an apparatus that is configured to look for the photon’s wave nature. So, the photon should – according to the standard way of thinking – go into a superposition of taking two paths. If the two paths are recombined, they interfere, and we get fringes. Now, said Wheeler, let’s perform a sleight of hand. Just before the photon is detected, let’s reconfigure the apparatus so that it’s now looking for the photon’s particle nature. This can be done by taking out the device that causes the paths to recombine, thus letting each path go on its way to separate detectors.
As it happens, you cannot fool the photon no matter how hard you try. Experimentalists have performed Wheeler’s thought experiment with increasing precision and sophistication – and the quantum world rules. When they remove, at the very last instant, the device that recombines the two photon paths, the photon acts like a particle, suggesting that it took one path or the other, even though at the start it should have entered a superposition of taking both paths at once. Based on such results, Wheeler argued that the photon has no intrinsic nature – either wave or particle – before it’s detected. Otherwise, if it entered the apparatus like a particle and you did a switcheroo nanoseconds before detection and chose to look at its wave nature, it would have to go back in time and re-enter the apparatus as a wave. How else can you explain the observed interference pattern? In Wheeler’s account, denying the photon a reality independent of observation avoids postulating absurd time-travelling photons, but then you have to live with the antirealism of standard quantum mechanics, which some find unpalatable.
Experimentalists have also combined delayed-choice and quantum-erasure experiments into one mind-boggling delayed-choice quantum-erasure experiment – in which you not only delay the choice of what to see (particle or wave nature), but you can also randomly erase this choice. Again, the photon or any quantum system will show you only one face or the other – and what it reveals depends on the final state of the experimental apparatus.
All particles in the Universe are influenced instantly by a form of nonlocality that would make Einstein wince
Such experiments suggest that the act of measurement collapses the wavefunction, but what does collapse really mean? Even more enigmatically, does collapse ultimately need observation by a conscious human being? (To be clear, almost no physicist today thinks that this is the case.)
To avoid the common sense-defying conceptual problems of standard quantum mechanics, there have been myriad attempts to reinterpret the results and pose new theories. One of these efforts is the so-called de Broglie-Bohm theory, which holds that reality is both a wave and a particle. In this theory, a particle is real and has a definite position at all times, and hence a trajectory; but the particle is guided by a pilot wave that evolves according to the Schrödinger equation. In the context of a double-slit experiment, the particle always goes through one slit or the other, but the pilot wave, or the wavefunction, goes through both and interferes with itself on the other side of the slits, and this interference pattern guides the particle to the photographic plate. The de Broglie-Bohm theory is realist: both particles and wavefunctions are real. But the theory is nonlocal. All particles – no matter where they are in the Universe – are influenced instantly by the evolving wavefunction, a form of extreme nonlocality that would make Einstein wince.
Yet another approach invokes a spontaneous collapse of the wavefunction, independent of observers or observation. Such theories are engineered so that small quantum systems, such as individual particles, can stay in a superposition of states for aeons, but larger agglomerations of particles – such as a cat – cannot, and so will almost instantaneously collapse into one of many probable states. Such theories predict that, as systems get bigger, spontaneous collapses will cause quantum states to become classical; they predict a mass scale at which this happens, dividing quantum reality from the classical world.
The quantum nanophysicist Markus Arndt and his colleagues at the University of Vienna are using the double-slit experiment to probe this divide by sending larger and larger things, such organic macromolecules and even viruses, through a double-slit to look for interference. If they see interference, the process is quantum mechanical. But if they can observe the disappearance of the interference pattern and show that it’s solely because the mass of the object going through the two slits is more than some threshold value, then they can claim to have found the quantum-classical divide. The search continues.
It’s hard to overstate the importance of the double-slit experiment to the entire enterprise of quantum mechanics, despite its astonishing simplicity and elegance.
As Feynman put it during a lecture at Cornell University in New York in 1964: ‘Any … situation in quantum mechanics, it turns out, can always be explained afterwards by saying: “You remember the case of the experiment with the two holes?”’ In 1964, even Feynman couldn’t have known just how important the experiment would turn out to be. But physics has yet to successfully explain the double-slit experiment. The case remains unsolved.