Rainbow over the Helford estuary, Cornwall, England. All photos courtesy Susanna Butterworth
This summer I went on a family holiday to Cornwall, on the Helford River. The peninsula south of the river is, rather wonderfully, called The Lizard. Standing on its cliffs, you are at the southernmost point of mainland Britain. North of the river is the port of Falmouth, from where packet-ships kept the mail services of the British Empire running until 1851. The area is lush with the sort of half-tamed beauty that England does so well, and the boundary with the contrasting wildness of the Atlantic is never far away.
Walking home from a riverside pub one evening, I witnessed a stirring natural display. With the Sun setting at our backs, a fantastically bright and complete double rainbow framed the river-opening leading out to the sea. I have always loved rainbows, and this was the best one I have seen. It even came in front of the horizon, past the trees on the riverbank opposite, and merged with its reflection in the river. It was an invitation and a dare to scientific understanding.
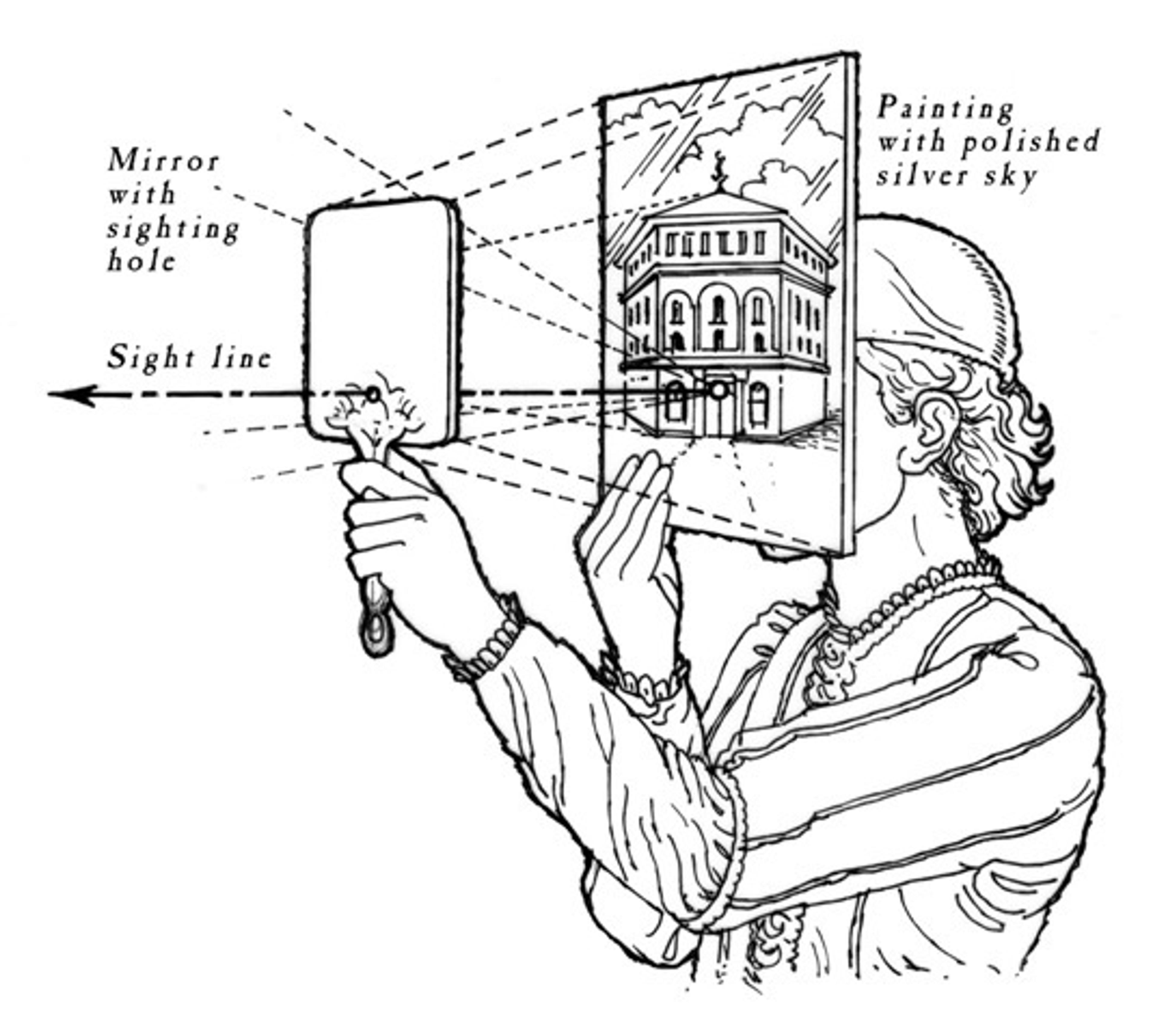
The image hovering in front of me was formed by sunlight streaming from behind us, internally reflected back towards us by myriad tiny suspended raindrops. When light meets an interface between air and water – the surface of a raindrop – some of it is reflected and some of it passes through. The angle of refraction depends both on the light’s wavelength and on the angle at which it hits the surface. Parallel rays entering a spherical raindrop bounce off the inside and come back towards us. The reflection angle from the back of the raindrop, combined with the two refractions (one as it enters the drop, and one as it leaves) conspire to concentrate each wavelength of light at a certain return angle. Wavelength corresponds to colour, so the colours separate into the familiar bands.
That is really all the physics you need to understand the basics of a rainbow. The first rainbow calculations were carried out by René Descartes back in 1637, although the dependence on wavelength, and hence the colours, needed Isaac Newton and Thomas Young’s later contributions. Although I already knew this history in principle, it was fresh in my mind because of a lovely review article by Alexander Haussmann of the Technical University in Dresden that I’d come across the same week. Haussmann’s review is full of both science and charm, and, unlike John Keats’s poor Lamia, the rainbow unwoven shines brighter for it.
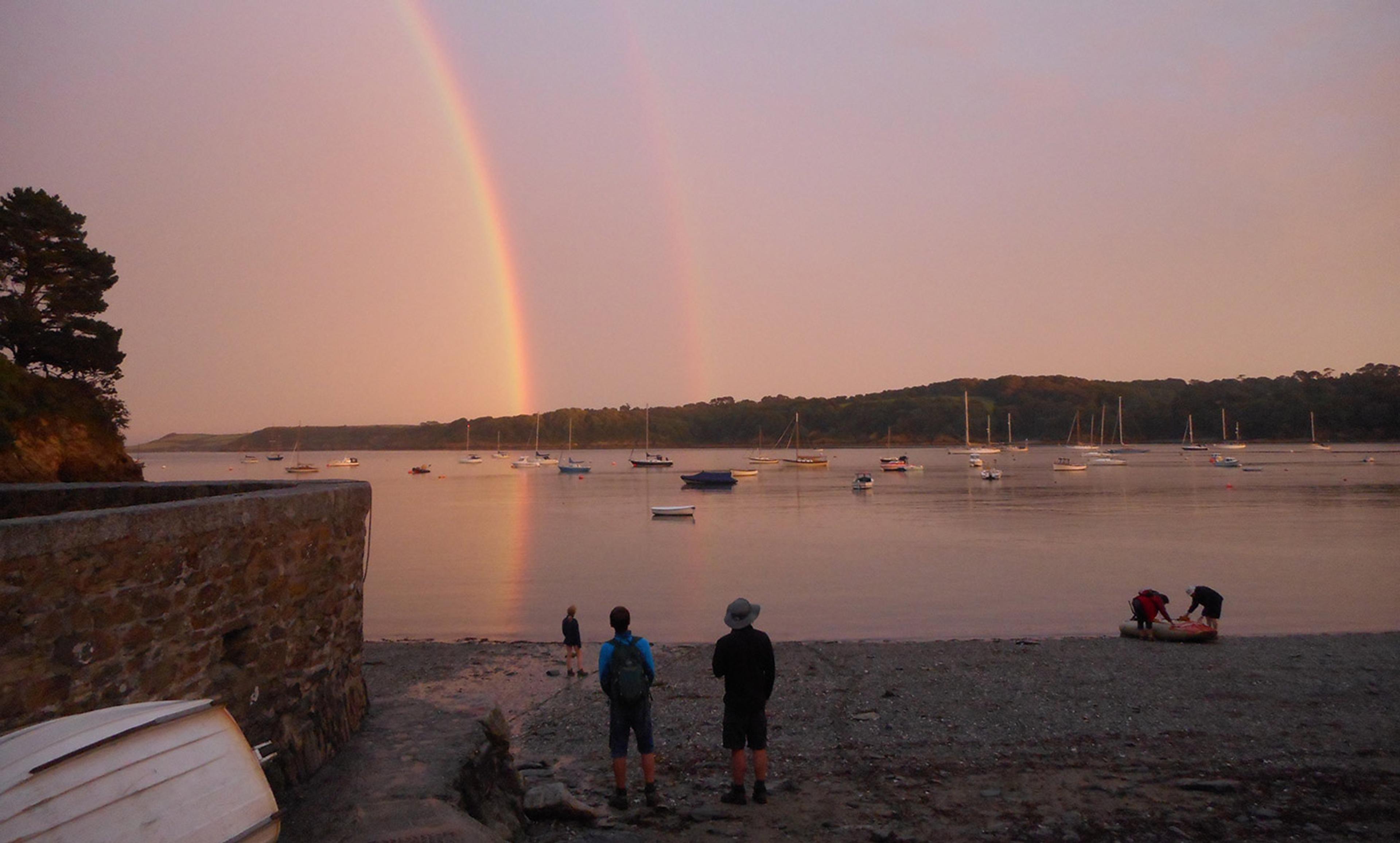
One thing adding to my wonder at the Cornwall rainbow was my realisation that the reflection I could see in the river was, despite appearances, not a reflection of the rainbow in the sky. A true reflection happens when light from the same object, but at a different angle, reaches the eye after bouncing off a surface. For instance, the clouds I could see mirrored in the surface of the river were true reflections. But a rainbow is made up from light reflected internally in raindrops and emitted at a specific angle; that is why we see the bow at all. It is not possible for the mirror image to be made from light reflected from the same drops, because it would have to have been emitted at a different angle in order to get to our eye. Instead, the mirror image comes from light from drops at a different position in the sky, radiated at the same angle.
Local changes in the rain shower can affect the mirror rainbow completely differently from the direct-view rainbow. There was more to that ‘reflection’ rainbow than met the eye, and there is more to a rainbow than the basic physics explanation, too.
As the theory of rainbows has developed over history, more odd or unusual features were explained. Not only was the separation of colours understood, but so was the presence of secondary rainbows that display their colours in the opposite order; these are caused by a double internal reflection within the raindrops. There is a darker band between the primary and secondary rainbows, known as ‘Alexander’s dark band’ after Alexander of Aphrodisias, who observed it around 200 AD. Alexander’s dark band lies at an angle forbidden by the optics of the simplest paths the light rays can travel along, making it darker than the rest of the sky. There are also rare ‘supernumerary arcs’ that can appear within the arc of the main bow, caused by interference between two light rays coming to the eye at the same angle but travelling slightly different distances.
All these features have been understood by developing Descartes’s original theory. The assumptions and approximations he made have been examined and refined, aided in recent years by increased computing power. Step by step, the details change and become more faithful to real life. You might think there is nothing left to learn about something so simple as a rainbow, but no – the process continues and has even picked up pace, as the ubiquity of high-quality digital cameras has yielded more and better images of startling, unusual rainbow features.
One recent example is a newfound appreciation of the importance of different drop sizes and shapes. The original theory of rainbows assumes perfectly spherical raindrops, and does not depend on the size of the drops. In reality, larger raindrops are squished flatter on the underside by air resistance as they fall, developing a shape that rainbow enthusiasts call the ‘hamburger bun’. Large drops usually make up a small fraction of a rain shower, but when they do contribute, calculations show that their oblateness leads to a change in the position of the top of the rainbow, while leaving the base unaffected. This is why the base of a rainbow often appears brighter than the top of the bow: all drop sizes contribute at the base, whereas near the top, light from the large, hamburger-bun drops is dispersed.
Using precise numerical calculations, performed on high-powered computers coded to describe the full scope of Maxwell’s equations of electromagnetism, increasingly esoteric features can be understood, and omissions and approximations in the theory can be fixed. That’s the way with science, whether we are talking about rainbows or high-energy particle collisions. Finding a flaw doesn’t mean the theory is worthless, but it does mean that the theory can be improved.
Scientists must avoid falling into the trap of defending all aspects of current thought because we feel the underlying truth needs protecting. Details of theory, or even broader aspects, can often be improved. Doing so strengthens the core of the theory – that is, if it is fundamentally correct. If it isn’t, then we need a better theory as soon as possible. The most effective way to find a deeper description of nature is to seek more observations and to push the existing conception to breaking point. All of those thoughts were hovering along with the rainbow over the Helford River.
Our understanding of rainbows is very robust now, but not complete. There are undoubtedly details that can still be improved. That walk home along the river, however, was definitely perfect.