Construction of the Manhattan Bridge, New York, 1909. Courtesy Library of Congress
The story of humanity is one of extraordinary cooperation but also terrible conflict. We come together to build cities, civilisations and cultures, but we also destroy these through violence against each other and degradation of our environment. Given that human nature is capable of both extremes, how can we design societies and institutions that help to bring out our better, more cooperative, instincts?
This question is not limited to humans. Life’s domains are replete with many forms of cooperation, from microbes sharing helpful molecules to dolphins providing aid to the injured. This kind of ‘altruistic’ behaviour – helping others at one’s own expense – presents an evolutionary puzzle. As Charles Darwin put it in The Descent of Man (1871): ‘He who was ready to sacrifice his life … rather than betray his comrades, would often leave no offspring to inherit his noble nature.’ The question then becomes, what kinds of conditions lead to the evolution of cooperative behaviour, when we would normally expect selfishness to prevail?
Ideas about evolution and human nature can be difficult to test in the laboratory. However, insight can come from a surprising place: mathematics. The idea is to create a mathematical model: a cartoon picture of the real world, drawn in the language of maths. Mathematical analysis can then provide a kind of ‘instant experiment’ to test an idea on its theoretical merits.
Of course, since any mathematical model excludes some features and oversimplifies others, we must be careful not to draw overly broad conclusions. History is littered with utopian ideas that looked great on paper but collapsed in practice. Still, mathematical modelling can be quite effective in separating promising ideas from those that are conceptually flawed.
Recently, I led a team of investigators to mathematically model how the structure of a society can encourage or suppress the evolution of cooperative behaviour. We represented structure as a network, in which every individual is linked to a certain set of ‘neighbours’. Links can be strong, as in the case of a close friend or family member, or weak, as for a rarely seen acquaintance.
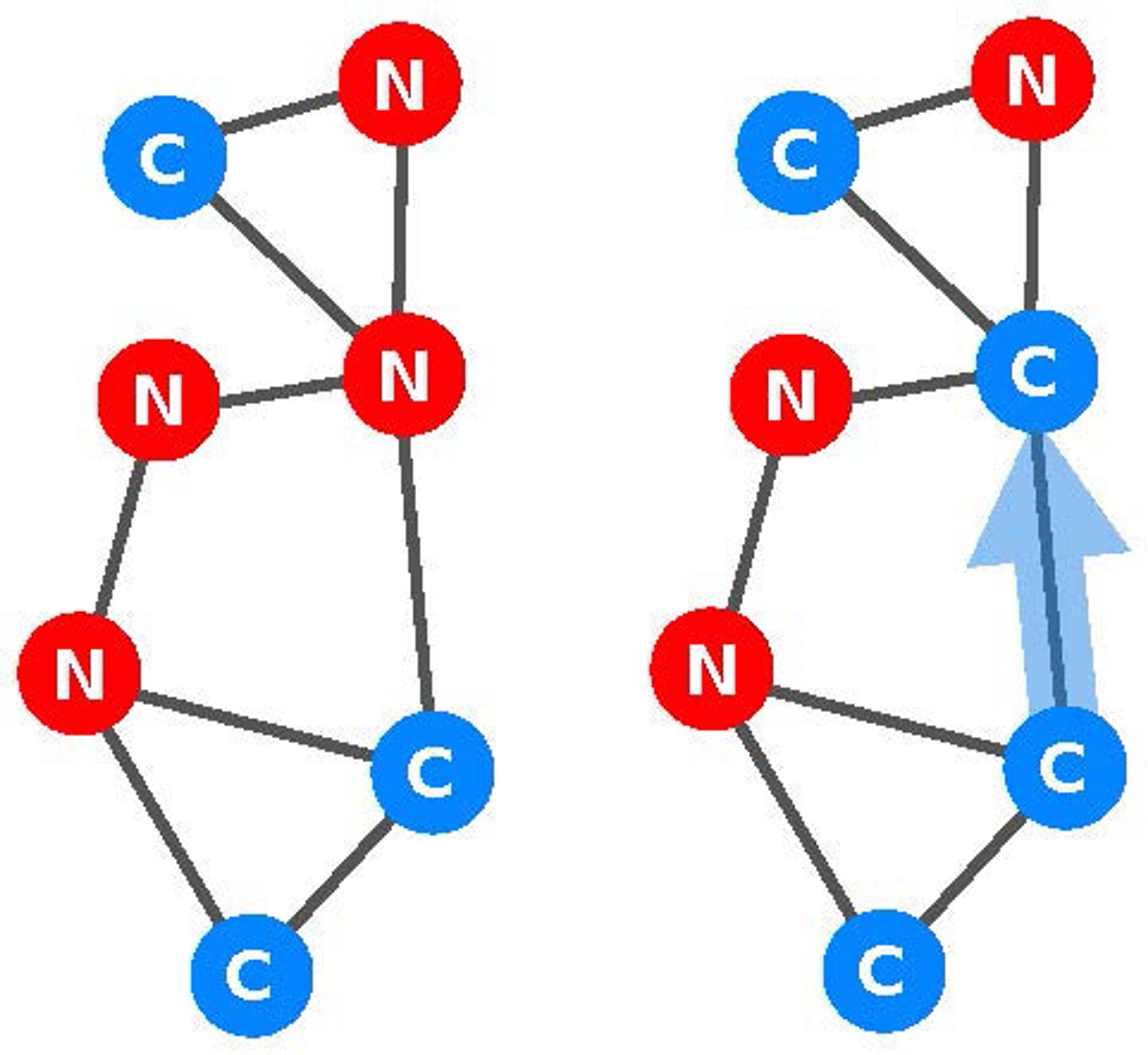
Fig 1. The two strategies, cooperation and non-cooperation, spread through the network as individuals imitate their neighbours
Individuals can cooperate, helping their neighbours at a cost to themselves, or not. This choice is an example of what game theory calls the ‘prisoner’s dilemma’. Each individual, if acting in pure self-interest, would choose not to cooperate. Yet cooperation by everyone leads to greater prosperity for all.
The two strategies, cooperation and non-cooperation, spread through the network as individuals imitate, or learn from, their neighbours. Individuals are more likely to imitate neighbours who do better in the prisoner’s dilemma. Over time, one strategy will win out: society will converge to a state where either everyone cooperates or no one does.
An earlier study had examined a simple case of this model, in which each individual has the same number of neighbours. They found that, for cooperation to flourish, the benefit-cost ratio of cooperation must be greater than the number of neighbours per individual. For example, if everyone has exactly five neighbours, cooperation succeeds if it provides at least five times as much benefit as the cost a cooperator pays. But while this is a beautiful result, its applicability is limited: in typical real-world networks, individuals differ widely in their number of neighbours, with some having a great many neighbours and others having very few.
We found a way to calculate whether cooperation is favoured on any network. The key quantity is the critical benefit-cost ratio. If this ratio is three, for example, then any cooperative behaviour providing a threefold-or-greater benefit is favoured. We showed how to calculate the critical cost-benefit ratio of any given network by solving a system of linear equations (a mathematically straightforward task). The smaller this ratio, the easier cooperation is to achieve. But for some networks, this ratio is negative, which means that cooperation is never favoured to evolve.
So which networks are best for promoting cooperation? Cooperation flourishes best when each individual has strong, reciprocated connections to a small number of others. In this case, cooperation spreads locally, along these connections, leading to clusters of cooperators who share benefits with each other. In contrast, if all individuals are equally connected to all others, the benefits of cooperation become diluted in the sea of non-cooperators, and the behaviour cannot spread. Thus, for cooperation to thrive, a few strong ties are better than a myriad weak ones.
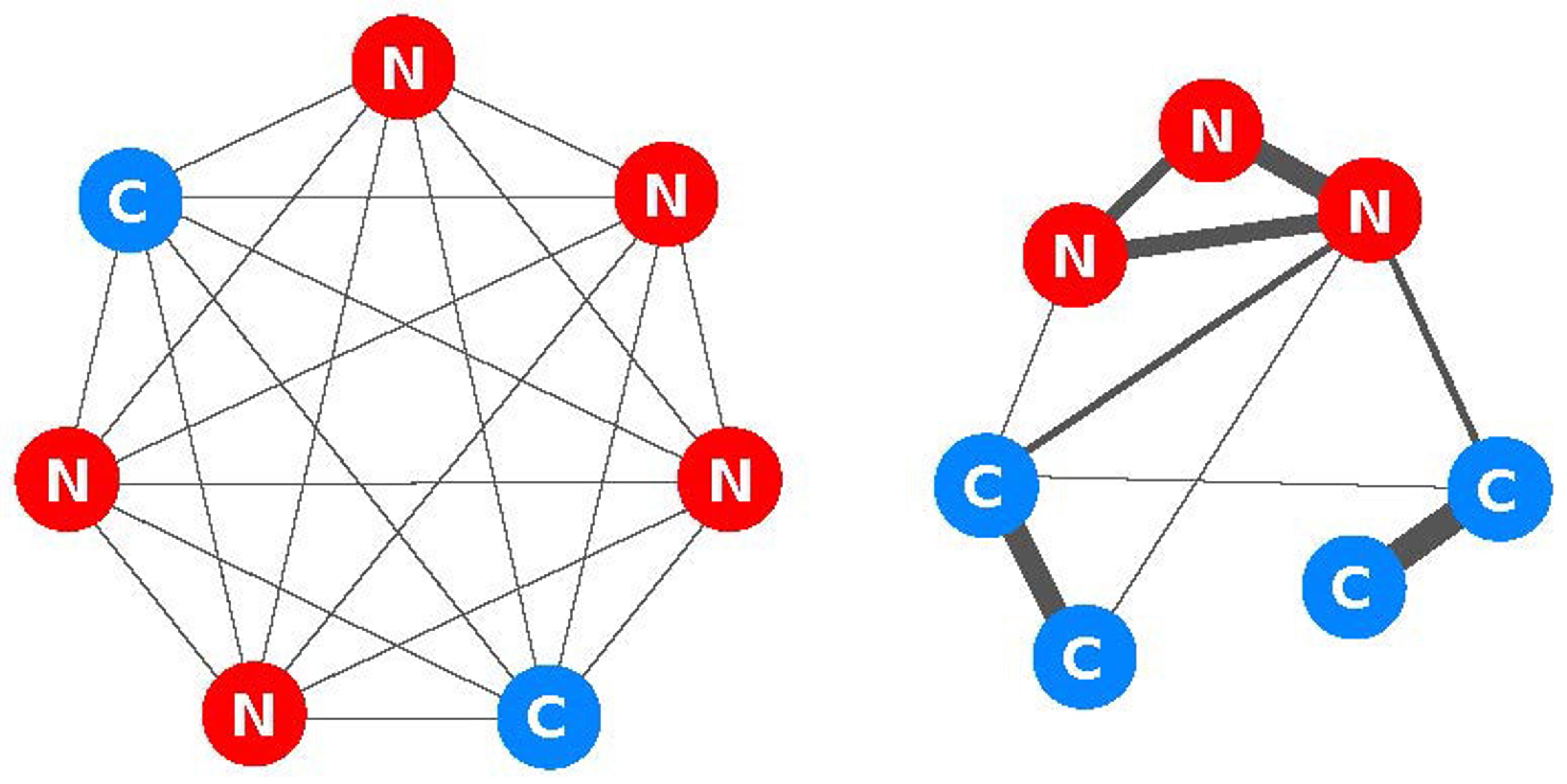
Fig 2. If everyone is equally connected to everyone else, cooperators are at a disadvantage. But if individuals have strong connections to only a few others, cooperation can spread locally to form clusters of mutual aid, eventually taking over the whole population
Humanity faces a number of unprecedented challenges. To respond to crises such as climate change, we must cooperate on a global scale. Mathematical modelling can help us design structures and institutions to make this cooperation possible. According to our model, open forums such as Twitter, in which anyone can interact with anyone else, might be great for sharing information, but terrible at promoting cooperation between users. Institutions that encourage fewer, stronger connections might have a better shot at getting individuals to work together for their common good.
This work is one step in a larger research programme to identify how structures, networks and interaction patterns can promote cooperation in biology and in society. Our model includes many simplifying assumptions that must be probed and tested to determine how widely our results apply. Much more work needs to be done – on paper, on computers, in the laboratory, and especially in the real world – to understand how we can design the networks that will best empower us to meet our collective challenges. Still, our simple, abstract model suggests a remarkably intuitive principle: the success of global cooperation depends on the strength of our local connections.






