Why can we count to 152? OK, most of us don’t need to stop there, but that’s my point. Counting to 152, and far beyond, comes to us so naturally that it’s hard not to regard our ability to navigate indefinitely up the number line as something innate, hard-wired into us.
Scientists have long claimed that our ability with numbers is indeed biologically evolved – that we can count because counting was a useful thing for our brains to be able to do. The hunter-gatherer who could tell which herd or flock of prey was the biggest, or which tree held the most fruit, had a survival advantage over the one who couldn’t. What’s more, other animals show a rudimentary capacity to distinguish differing small quantities of things: two bananas from three, say. Surely it stands to reason, then, that numeracy is adaptive.
But is it really? Being able to tell two things from three is useful, but being able to distinguish 152 from 153 must have been rather less urgent for our ancestors. More than about 100 sheep was too many for one shepherd to manage anyway in the ancient world, never mind millions or billions.
The cognitive scientist Rafael Núñez of the University of California at San Diego doesn’t buy the conventional wisdom that ‘number’ is a deep, evolved capacity. He thinks that it is a product of culture, like writing and architecture. ‘Some, perhaps most, scholars endorse a nativist view that numbers are biologically endowed,’ he said. ‘But I’d argue that, while there’s a biological grounding, language and cultural traits are necessary for the establishment of number itself.’
‘The idea of an inherited number sense as the unique building block of complex mathematical skill has had an unusual attraction,’ said the neuroscientist Wim Fias of the University of Gent in Belgium. ‘It fits the general enthusiasm and hope to expect solutions from biological explanations,’ in particular, by coupling ‘the mystery of human mind and behaviour with the promises offered by genetic research.’ But Fias agrees with Núñez that the available evidence – neuroscientific, cognitive, anthropological – just doesn’t support the idea.
If Núñez and Fias are right, though, where does our sense of number come from? If we aren’t born equipped with the neural capacity for counting, how do we learn to do it? Why do we have the concept of 152?
‘Understanding number as a quantity is the most essential, most basic part of mathematical knowledge,’ explained Fias. Yet numbers seem to be out there in the world, no less than atoms and galaxies; they seem to be pre-existing things just awaiting discovery. The great insights of mathematics, especially in number theory, are simply found to be true (or not). That 32 + 42 = 52 is a delightful property of numbers themselves, not an invention of Pythagoras.
Yet whether numbers really exist independently of humans ‘is not a scientific debate, but a philosophical, theological or ideological one’, said Núñez. ‘The claim that, say, five is a prime number independently of humans is not scientifically testable. Such facts are matters of beliefs or faith, and we can have conversations and debates about them but we cannot do science with them.’
Still, it seems puzzling that we can figure out these things at all. Geometry and basic arithmetic were handy tools for the ancient builders and lawmakers – ‘geometry’, after all, means ‘measuring the Earth’ – but it’s hard to see how they served any function as human cognition was evolving over the previous million or more years. There certainly was no biological need to be able to prove Fermat’s last theorem, or even to state it in the first place.
To explore such dizzying questions of number theory, even the most gifted mathematicians have to start in the same place as the rest of us: by learning to count to 10. To do that, we need to know what numbers are. Once we know that the abstract symbol ‘five’ equates with the number of fingers on our hand, and that this is one more than the ‘four’ that equates to the number of legs on a dog, we have the foundations of arithmetic.
The capacity to discriminate between different quantities happens extremely quickly in the development of a child – before we even have words to express it. A baby just three or four days old can show by its responses that it can discern the difference between two items and three, and by four months or so babies can grasp that the number of items you get by grouping one of them with another one is the same as two of them. They have a sense of the elementary operation that they will later learn to express as the arithmetic formula 1+1=2.
Our capacity for tennis doesn’t mean that we evolved to play it, or that we have a tennis module in our brain
Monkeys, chimps, dolphins and dogs can likewise tell which of two groups of food items has more, if the numbers are below 10. Even pigeons ‘can be trained to press a certain amount of times on a lever to obtain food’, said Fias.
Such observations gave rise to what has long been the predominant view that we humans are born with an innate sense of number, says the cognitive neuroscientist Daniel Ansari of the University of Western Ontario in London, Canada. The neuroscientific evidence seemed to offer strong support for that view. For example, Ansari said: ‘Studies with newborns and infants show that, if you show them eight dots repeatedly and then change it to 16 dots, areas in the right parietal cortex of the brain respond to a change in numerosity. This response is very similar in adults.’ Some researchers have concluded that we are born with a ‘number module’ in our brains: a neural substrate that supports later learning of our culture’s symbolic system of representing and manipulating numbers.
Not so fast, responds Núñez. Just because a behaviour seems to derive from an innate capacity, that doesn’t mean the behaviour is itself innate. Playing tennis makes exquisite use of our evolutionary endowment (present company excepted). We can coordinate our eyes and muscles not just to make contact between ball and racket but also to knock the ball into the opposite corner from our opponent. Most impressively, we can read the trajectory of a ball, sometimes at fantastic speed, so that our racket is precisely where the ball is going to be when it reaches us. But this capacity doesn’t mean that our early ancestors evolved to play tennis, or that we have some kind of tennis module in our brains. ‘The biologically evolved preconditions making some activity X possible, whether it’s numbers or snowboarding, are not necessarily the “rudiments of X”,’ explained Núñez.
Numerical ability is more than a matter of being able to distinguish two objects from three, even if it depends on that ability. No non-human animal has yet been found able to distinguish 152 items from 153. Chimps can’t do that, no matter how hard you train them, yet many children can tell you even by the age of five that the two numbers differ in the same way as do the equally abstract numbers 2 and 3: namely, by 1.
What seems innate and shared between humans and other animals is not this sense that the differences between 2 and 3 and between 152 and 153 are equivalent (a notion central to the concept of number) but, rather, a distinction based on relative difference, which relates to the ratio of the two quantities. It seems we never lose that instinctive basis of comparison. ‘Despite abundant experience with number through life, and formal training of number and mathematics at school, the ability to discriminate number remains ratio-dependent,’ said Fias.
What this means, according to Núñez, is that the brain’s natural capacity relates not to number but to the cruder concept of quantity. ‘A chick discriminating a visual stimulus that has what (some) humans designate as “one dot” from another one with “three dots” is a biologically endowed behaviour that involves quantity but not number,’ he said. ‘It does not need symbols, language and culture.’
‘Much of the “nativist” view that number is biologically endowed,’ Núñez added, ‘is based on the failure to distinguish at least these two types of phenomena relating to quantity.’ The perceptual rough discrimination of stimuli differing in ‘numerousness’ or quantity, seen in babies and in other animals, is what he calls quantical cognition. The ability to compare 152 and 153 items, in contrast, is numerical cognition. ‘Quantical cognition cannot scale up to numerical cognition via biological evolution alone,’ Núñez said.
Although researchers often assume that numerical cognition is inherent to humans, Núñez points out that not all cultures show it. Plenty of pre-literate cultures that have no tradition of writing or institutional education, including indigenous societies in Australia, South America and Africa, lack specific words for numbers larger than about five or six. Bigger numbers are instead referred to by generic words equivalent to ‘several’ or ‘many’. Such cultures ‘have the capacity to discriminate quantity, but it is rough and not exact, unlike numbers’, said Núñez.
That lack of specificity doesn’t mean that quantity is no longer meaningfully distinguished beyond the limit of specific number words, however. If two children have ‘many’ oranges but the girl evidently has lots more than the boy, the girl might be said to have, in effect, ‘many many’ or ‘really many’. In the language of the Munduruku people of the Amazon, for example, adesu indicates ‘several’ whereas ade implies ‘really lots’. These cultures live with what to us looks like imprecision: it really doesn’t matter if, when the oranges are divided up, one person gets 152 and the other 153. And frankly, if we aren’t so number-fixated, it really doesn’t matter. So why bother having words to distinguish them?
Some researchers have argued that the default way that humans quantify things is not arithmetically – one more, then another one – but logarithmically. The logarithmic scale is stretched out for small numbers and compressed for larger ones, so that the difference between two things and three can appear as significant as the difference between 200 and 300 of them.
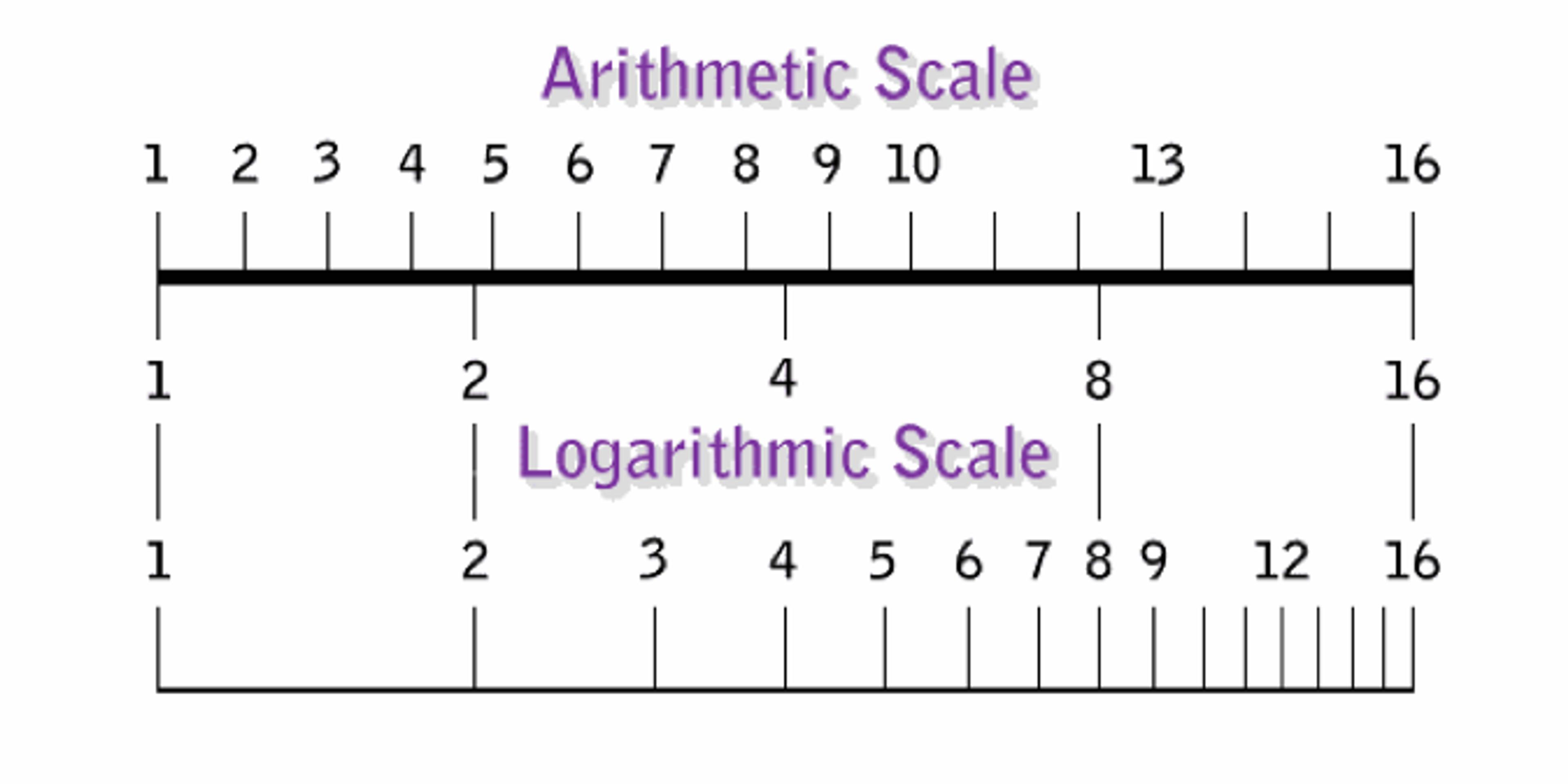
The arithmetic and logarithmic scales for numbers up to 16. The higher you go on the arithmetic scale, the more the logarithmic scale gets compressed.
In 2008, the cognitive neuroscientist Stanislas Dehaene of the Collège de France in Paris and his coworkers reported evidence that the Munduruku system of accounting for quantities corresponds to a logarithmic division of the number line. In computerised tests, they presented a tribal group of 33 Munduruku adults and children with a diagram analogous to the number line commonly used to teach primary-school children, albeit without any actual number markings along it. The line had just one circle at one end and 10 circles at the other. The subjects were asked to indicate where on the line groupings of up to 10 circles should be placed.
Whereas Western adults and children will generally indicate evenly spaced (arithmetically distributed) numbers, the Munduruku people tended to choose a gradually decreasing spacing as the numbers of circles got larger, roughly consistent with that found for abstract numbers on a logarithmic scale. Dehaene and colleagues think that for children to learn to space numbers arithmetically, they have to overcome their innately logarithmic intuitions about quantity.
Maybe the industrialised cultures are odd, with their pedantic distinction between 1,000,002 and 1,000,003
Attributing more weight to the difference between small than between large numbers makes good sense in the real world, and fits with what Fias says about judging by difference ratios. A difference between families of two and three people is of comparable significance in a household as a difference between 200 and 300 people is in a tribe, while the distinction between tribes of 152 and 153 is negligible.
It’s easy to read this as a ‘primitive’ way of reasoning, but anthropology has long dispelled such patronising prejudice. After all, some cultures with few number words might make much more fine-grained linguistic distinctions than we do for, say, smells or family hierarchies. You develop words and concepts for what truly matters to your society. From a practical perspective, one could argue that it’s actually the somewhat homogeneous group of industrialised cultures that look odd, with their pedantic distinction between 1,000,002 and 1,000,003.
Whether the Munduruku really map quantities onto a quasi-logarithmic division of ‘number space’ is not clear, however. That’s a rather precise way of describing a broad tendency to make more of small-number distinctions than of large-number ones. Núñez is skeptical of Dehaene’s claim that all humans conceptualise an abstract number line at all. He says that the variability of where Munduruku people (especially the uneducated adults, who are the most relevant group for questions of innateness versus culture) placed small quantities on the number line was too great to support the conclusion about how they thought of number placement. Some test subjects didn’t even consistently rank the progressive order of the equivalents of 1, 2 and 3 on the lines they were given.
‘Some individuals tended to place the numbers at the extremes of the line segment, disregarding the distance between them,’ said Núñez. ‘This violates basic principles of how the mapping of the number line works at all, regardless of whether it is logarithmic or arithmetic.’
Building on the clues from anthropology, neuroscience can tell us additional details about the origin of quantity discrimination. Brain-imaging studies have revealed a region of the infant brain involved in this task – distinguishing two dots from three, say. This ability truly does seem to be innate, and researchers who argue for a biological basis of number have claimed that children recruit these neural resources when they start to learn their culture’s symbolic system of numbers. Even though no one can distinguish 152 from 153 randomly spaced dots visually (that is, without counting), the argument is that the basic cognitive apparatus for doing so is the same as that used to tell 2 from 3.
But that appealing story doesn’t accord with the latest evidence, according to Ansari. ‘Surprisingly, when you look deeply at the patterns of brain activation, we and others found quite a lot of evidence to suggest a large amount of dissimilarity between the way our brains process non-symbolic numbers, like arrays of dots, and symbolic numbers,’ he said. ‘They don’t seem to be correlated with one another. That challenges the notion that the brain mechanisms for processing culturally invented number symbols maps on to the non-symbolic number system. I think these systems are not as closely related as we thought.’
If anything, the evidence now seems to suggest that the cause-and-effect relationship works the other way: ‘When you learn symbols, you start to do these dot-discrimination tasks differently.’
This picture makes intuitive sense, Ansari argues, when you consider how hard kids have to work to grasp numbers as opposed to quantities. ‘One thing I’ve always struggled with is that on the one hand we have evidence that infants can discriminate quantity, but on the other hand it takes children between two to three years to learn the relationship between number words and quantities,’ he said. ‘If we thought there was a very strong innate basis on to which you just map the symbolic system, why should there be such a protracted developmental trajectory, and so much practice and explicit instruction necessary for that?’
But the apparent disconnect between the two types of symbolic thought raises a mystery of its own: how do we grasp number at all if we have only the cognitive machinery for the cruder notion of quantity? That conundrum is one reason why some researchers can’t accept Núñez’s claim that the concept of number is a cultural trait, even if it draws on innate dispositions. ‘The brain, a biological organ with a genetically defined wiring scheme, is predisposed to acquire a number system,’ said the neurobiologist Andreas Nieder of the University of Tübingen in Germany. ‘Culture can only shape our number faculty within the limits of the capacities of the brain. Without this predisposition, number symbols would lie [forever] beyond our grasp.’
If you’re inherently good at assessing numbers visually, you’ll be good at maths
‘This is for me the biggest challenge in the field: where do the meanings for number symbols come from?’ Ansari asks. ‘I really think that a fuzzy system for large quantities is not going to be the best hunting ground for a solution.’
Perhaps what we draw on, he thinks, is not a simple symbol-to-quantity mapping, but a sense of the relationships between numbers – in other words, a notion of arithmetical rules rather than just a sense of cardinal (number-line) ordering. ‘Even when children understand the cardinality principle – a mapping of number symbols to quantities – they don’t necessarily understand that if you add one more, you get to the next highest number,’ Ansari said. ‘Getting the idea of number off the ground turns out to be extremely complex, and we’re still scratching the surface in our understanding of how this works.’
The debate over the origin of our number sense might itself seem rather abstract, but it has tangible practical consequences. Most notably, beliefs about the relative roles of biology and culture can influence attitudes toward mathematical education.
The nativist view that number sense is biological seemed to be supported by a 2008 study by researchers at the Johns Hopkins University in Baltimore, which showed 14-year-old test subjects’ ability to discriminate at a glance between exact numerical quantities (such as the number of dots in an image) correlated with their mathematics test scores going back to kindergarten. In other words, if you’re inherently good at assessing numbers visually, you’ll be good at maths. The findings were used to develop educational tools such as Panamath to assess and improve mathematical ability.
But Fias says that such tests of supposedly innate discrimination between numbers of things aren’t as solid as they might seem. It’s impossible to separate out the effects of the number of dots from factors such as their density, areal coverage and brightness. Researchers have known since the studies of the child-development guru Jean Piaget in the 1960s that young children don’t instinctively judge number independently from conflicting visual features. For instance, they’ll say that a row of widely space marbles contains more than a densely spaced (and hence shorter) row with the same number. Furthermore, many studies show that arithmetic skill is more closely linked to learning and understanding of number symbols (1, 2, 3…) than to an ability to discriminate numbers of objects visually.
As much as educators (and the researchers themselves) desire firm answers, the truth is that the debate about the origin of numerical cognition is still wide open. Nieder remains convinced that ‘our faculty for symbolic number, no matter how much more elaborate than the non-symbolic capacity of animals, is part of our biological heritage’. He feels that Núñez’s assertion that numbers themselves are cultural inventions ‘is beyond the reach of experimental investigation, and therefore irrelevant from a scientific point of view’. And he believes that a neurobiological foundation of numerosity is needed to understand why some people suffer from dyscalculia – an inability of the brain to deal with numbers. ‘Only with a neurobiological basis of the number faculty can we hope to find educational and medical therapies’ for such cases, he said.
But if Núñez is right that the concept of number is a cultural elaboration of a much cruder biological sense of quantity, that raises new and intriguing questions about mathematics in the brain. How and why did we decide to start counting? Did it begin when we could name numbers, perhaps? ‘Language in itself may be a necessary condition for number, but it is not sufficient for it,’ said Núñez. ‘All known human cultures have language, but by no means all have exact quantification in the form of number.’
‘How and when the transition from quantical to numerical thinking happened is hard to unravel,’ said Andrea Bender, a cognitive scientist at the University of Bergen in Norway, ‘especially if one assumes that language played a pivotal role in this process, because we don’t even know when language emerged. All research in developmental psychology seems to indicate that one needs to have culture before one can understand number concepts.’ Some archaeologists date numerical thinking back to the Palaeolithic era a few tens of thousands of years ago, Bender said, based on material remains such as notched bones or finger stencils – ‘but this is speculative to some extent’.
The digital age has made binary seem perfectly logical: what works best depends on what you want to do
Further complicating things, when different cultures developed the concept of number, they came up with varying solutions of how best to count. Although many Western languages count in base 10 – probably guided by the number of digits on our hands – they typically have a language rooted in a base-12 calendar, so that only at 13 (‘three-ten’) do the number words become composite. Chinese was more logical and consistent from the start, denoting 11 in characters as ‘ten-one’ and continuing that logical structure to higher orders, with 21 being ‘two-ten-one’ and so forth. Some researchers have claimed that this relative linguistic transparency accounts for China’s impressive numeracy (although the difficulty of the written script works in the other direction for literacy).
Or we could have adopted a different number system altogether. Take the people of the small island of Mangareva in French Polynesia. Bender and her coworkers found that the Mangarevans use a counting system that is a mixture of the familiar decimal system and another that is equivalent to binary. That might have seemed a peculiar choice before the digital age, which has made binary seem, well, perfectly logical. But which number system works best depends on what you want to do with numbers, Bender says.
For certain arithmetical operations involved in the distribution of food and provisions in Mangarevan society, binary can be simpler to use. In this setting, at least, it’s a good solution to a cultural problem. ‘Mangarevan and related Polynesian cultures seem to be great examples of inventing counting systems because they were more efficient for the tasks at hand,’ Bender said.
She feels that her findings support Núñez’s contention that, although humans have biological, evolved preconditions for numerical cognition, ‘the tools they need and invent are a product of culture, and hence are diverse’.
Núñez thinks that many of his colleagues might be too eager to attribute to biology and evolution certain capacities that also derive from culture, such as music. ‘Many animals have capacities for sound discrimination, for vocalising with various frequencies and intensities, and so on,’ he said. ‘That doesn’t necessarily mean that those are “rudiments of music”. Vocal tracts are needed for bel canto, but they did not evolve for bel canto.’
Perhaps at the root of the impassioned disputes over number sense is a desire to valorise certain traits and capacities – not just mathematics, but also art and music – by giving them a naturalistic imprimatur of biology, as if they would be somehow diminished otherwise. Certainly, the fierceness of arguments triggered by the cognitive scientist Steven Pinker’s proposal that music is parasitic on capacities evolved for other reasons – he called it ‘auditory cheesecake’ – betrayed a sense that the intrinsic worth of music itself was at stake.
Which is odd, when you come to think about it. The idea that a grand mental capacity comes from our culture – that we conjured up something beyond our immediate biological endowment, through the sheer power of thought – seems rather ennobling, not dismissive. Perhaps we should give ourselves more credit.