Almost a century ago, physics produced a problem child, astonishingly successful yet profoundly puzzling. Now, just in time for its 100th birthday, we think we’ve found a simple diagnosis of its central eccentricity.
This weird wunderkind was ‘quantum mechanics’ (QM), a new theory of how matter and light behave at the submicroscopic level. Through the 1920s, QM’s components were assembled by physicists such as Werner Heisenberg and Erwin Schrödinger. Alongside Albert Einstein’s relativity theory, it became one of the two great pillars of modern physics.
The pioneers of QM realised that the new world they had discovered was very strange indeed, compared with the classical (pre-quantum) physics they had all learned at school. These days, this strangeness is familiar to physicists, and increasingly useful for technologies such as quantum computing.
The strangeness has a name – it’s called entanglement – but it is still poorly understood. Why does the quantum world behave this strange way? We think we’ve solved a central piece of this puzzle.
Entanglement was first clearly described, and named, in 1935, by the Austrian physicist Erwin Schrödinger. He pointed out that, after two quantum particles interacted, they could no longer be considered independent of each other, as classical physics would have allowed. As the contemporary US physicist Leonard Susskind puts it in the preface to Quantum Mechanics: The Theoretical Minimum (2014), ‘one can know everything about a system and nothing about its individual parts.’
Here’s a simple analogy. If we want to give a complete description of the present state of a two-handed poker game, for example, we just give a description of the two five-card hands. What could be more obvious? But in QM, for some reason, the obvious thing doesn’t work.
Schrödinger said that, in general, the quantum description of the two particles is ‘entangled’, and the name stuck. As he puts it: ‘When two separated bodies that each are maximally known come to interact, and then separate again, then such an entanglement of knowledge often happens.’
The full weirdness of entanglement wasn’t immediately obvious
Schrödinger concluded elsewhere that entanglement is not ‘one but rather the characteristic trait of quantum mechanics.’ Many physicists now agree. Susskind says it is ‘the essential fact of quantum mechanics’, while in his Lectures on Quantum Mechanics (2013), Steven Weinberg writes that it is ‘perhaps its weirdest feature’.
The full weirdness of entanglement wasn’t immediately obvious, and Schrödinger himself didn’t quite live to see it. For him, its strangeness was the prohibition it imposed on describing a two-particle system by its parts. He thought that this had important consequences, especially because it debunked what had become the orthodox view of what QM is telling us about the microworld.
This orthodox view was the so-called Copenhagen Interpretation, proposed by the Danish physicist Niels Bohr. Bohr argued that it was nonsense to think of quantum systems as having definite properties, before they were measured. Like Einstein before him, Schrödinger thought that entanglement proved Bohr wrong.
To grasp the Einstein-Schrödinger argument, consider the two poker hands, now with some of the cards face down, hidden from view. The state of this game can no longer be described in terms of the known cards (the ones turned face up). At least superficially, this looks like entanglement: a full quantum system can’t be described in terms of what’s known about its pieces.
Moreover, when an additional card on one side is revealed, it changes our knowledge about the other hand. If the queen of hearts turns up in the hand on the left, say, then we know that it is not one of the hidden cards in the hand on the right. The same is true for entangled particles. Observing one gives us new knowledge about the other, even if it is a long way away.
Einstein and Schrödinger argued that this meant that something is hidden inside these quantum systems prior to measurement – something not fully described by QM, and disallowed by Bohr’s view. They argued that, if measuring a nearby particle teaches us a new fact about a remote particle, this new fact must have existed already, even though the best QM description didn’t include it.
The alternative would be that the nearby measurement was changing the remote particle in some way. Schrödinger thought that this was absurd: ‘measurements on separated systems cannot affect one another directly, that would be magic [our emphasis].’
‘It provides a gentle pillow for the true believer from which he cannot very easily be aroused’
Schrödinger died in Vienna in 1961. Just three years later, the Northern Irish physicist John Stewart Bell argued that, if the predictions of QM are correct, then Schrödinger’s magic actually happens. When we have entangled particles, measurements on one of them can have a subtle effect on the other one, even though they might in principle be light years apart.
Bell called this magic nonlocality. These days it is often linked to Einstein’s phrase ‘spooky action at a distance’, though Einstein, too, didn’t live to see Bell’s result. (When Einstein complained about spooky action at a distance, in a 1947 letter to the physicist Max Born, he had in mind a different weird feature of the orthodox interpretation of QM.)
The importance of Bell’s argument took some time to sink in. The field had to first shake off some of what Einstein in 1928, writing to Schrödinger, called the ‘Heisenberg-Bohr tranquilising philosophy … so delicately contrived that, for the time being, it provides a gentle pillow for the true believer from which he cannot very easily be aroused.’
But gradually, in the second half of the quantum century, entanglement became one of the major concerns of the field. It is now absolutely central, theoretically, experimentally and, increasingly, technologically. Entanglement is what makes quantum computers different from their classical cousins, for example. A major motivation for this shift was Bell’s work. As the physicist Krister Shalm put it to Quanta Magazine in 2021: ‘The quantum revolution that’s happening now, and all these quantum technologies – that’s 100 per cent thanks to Bell’s theorem.’
Bell had argued that, if the QM predictions were correct, then nonlocality was unavoidable. But were the predictions correct? Answering that question required some very subtle and difficult experiments, involving two-particle systems similar to those that Schrödinger had discussed in 1935. Since they were inspired by Bell’s work, they came to be called ‘Bell experiments’.
Most Bell experiments use photons, the fundamental quantum components of light. Pairs of photons are produced together, with their properties entangled in the way that Schrödinger had described. Each photon is sent to one of two physicists, conventionally called Alice and Bob. Alice and Bob each choose one of several available measurements – this is called choosing a measurement setting.
Each measurement produces an outcome, which might be a 1 or a 0, depending on which way the photon emerges from the measuring device. Each run of the experiment thus produces four numbers: the two settings and the two outcomes. Repeated over and over, the experiment generates a long table of results, with these four numbers in each row.
Bell realised that these experimental results, as predicted by QM, looked quite strange. So strange, in fact, that with just a few additional assumptions, he could prove that the results were impossible. The primary assumption was that Schrödinger’s magic was not allowed – Bell called this assumption locality. So if QM’s predictions were correct after all, that would be bad news for locality (and good news for magic).
‘This is the real problem with quantum theory: the apparently essential conflict [with] fundamental relativity’
It took several decades, but we now know that QM is indeed correct. Some of the most convincing Bell experiments were conducted as recently as 2015. In 2022, nicely timed for the decade of quantum centenaries, the Nobel Prize in Physics was awarded to three pioneers of these experiments: Alain Aspect, John Clauser and Anton Zeilinger. As the Nobel citation put it, the prize recognised their ‘experiments with entangled photons, establishing the violation of Bell inequalities and pioneering quantum information science.’
Combined with these experiments, Bell’s analysis seems to imply the kind of magical action at a distance that Einstein and Schrödinger considered absurd. One reason for thinking that it would be absurd was that it would seem to clash with a core principle of Einstein’s own theory of relativity – that nothing could go faster than light.
Bell was well aware of this tension, saying in 1984 that there was ‘an apparent incompatibility, at the deepest level’, between QM and relativity. ‘For me then,’ he said, ‘this is the real problem with quantum theory: the apparently essential conflict [with] fundamental relativity.’ Forty years later, this conflict has not been resolved.
The work of Aspect, Clauser and Zeilinger and many others certainly confirms that entanglement is real. As Aspect himself put it in his speech at the Nobel Prize banquet: ‘Entanglement is confirmed in its strangest aspects.’ But the experiments don’t tell us what entanglement is, or where it comes from. In that sense, entanglement remains as mysterious as ever. Why is the world put together in this weird way?
Our research suggests a surprisingly simple answer. Our recipe for producing entanglement uses just four ingredients. All of these ingredients are available off the shelf (although admittedly, in one case, from a remote corner of the shelf). As far as we know, it has not previously been noticed that they can be combined in this way, to throw new light on the weirdest feature of the quantum world.
Let’s start with the main ingredient. Called collider bias, it is well known to scientists who use statistics in fields such as sociology, psychology and medicine. One of the first writers to describe it clearly was Joseph Berkson, a Mayo Clinic physicist, physician and statistician. In the 1940s, Berkson noted an important source of error in statistical reasoning used in medicine. In some circumstances, the selection of a sample of patients produces misleading correlations between their medical conditions.
Simplifying Berkson’s own example, imagine that all the patients admitted to hospital Ward C have similar symptoms, caused by one of two rare infections, Virus A or Virus B. Ward C specialises in treating those symptoms, so all its patients have at least one of these diseases. A few may have both, but everyone on the ward who doesn’t have Virus A is certain to have Virus B, and vice versa.
Taken at face value, these correlations might suggest that avoiding one virus causes infection with the other one. But Berkson pointed out that this apparent causal connection isn’t real. It is an artefact of the way the sample has been selected. The patients on Ward C are a very biased sample. In the general population, having a vaccine for Virus A won’t make you more likely to catch Virus B.
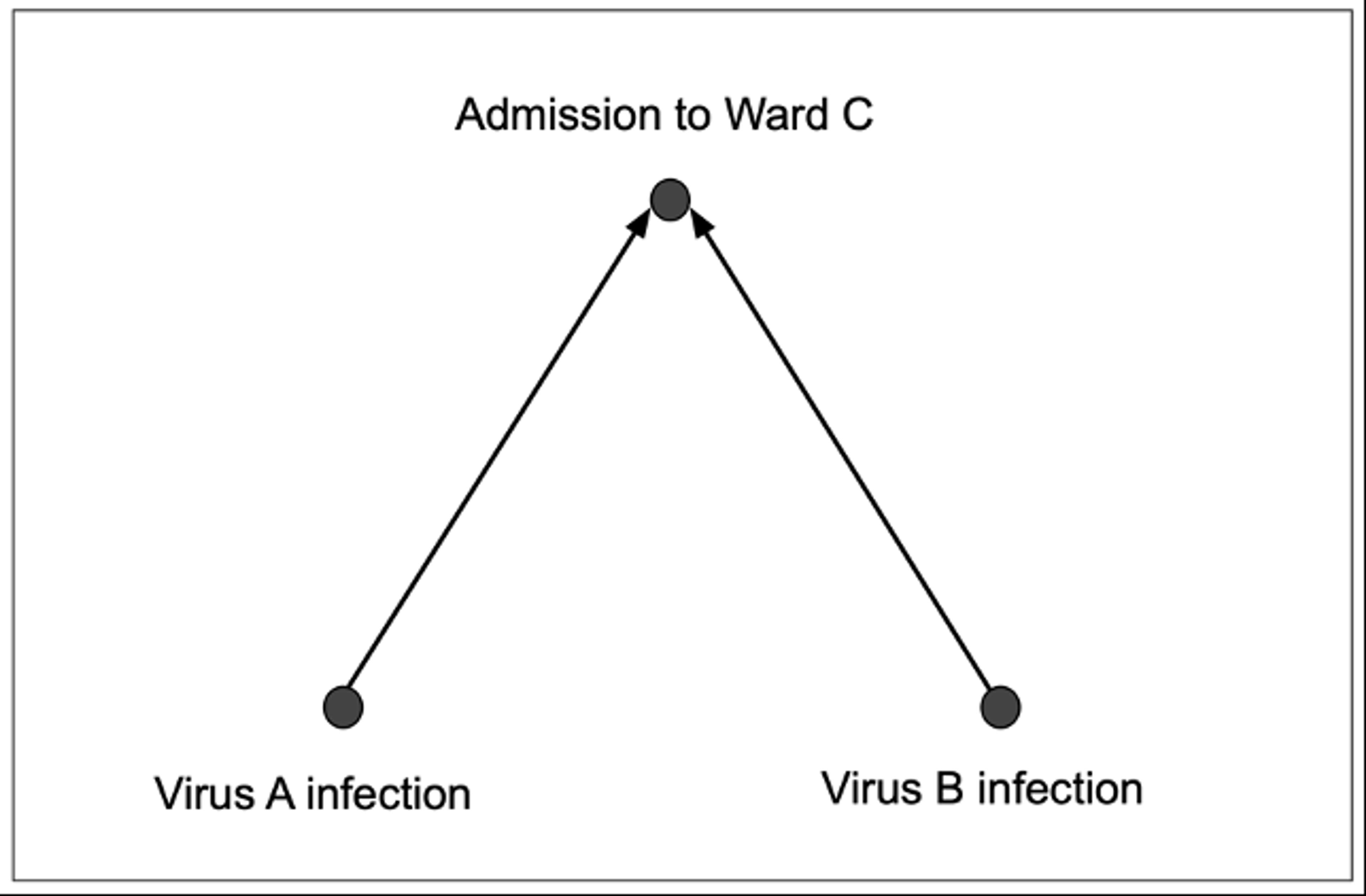
Figure 1: a simple collider
This means that if a patient on Ward C with Virus A says to himself: ‘I’m on Ward C, so, if I hadn’t caught Virus A, I would have caught Virus B,’ then he’s making a mistake. If he hadn’t caught Virus A then (most likely) he wouldn’t have either virus, and he wouldn’t have been admitted to the ward.
It may look like these causes are influencing one another, but they are not
This statistical effect is now called Berkson’s bias, or collider bias. The term collider comes from causal modelling, the science of inferring causes from statistical data. Causal modellers use diagrams called directed acyclic graphs (DAGs), made up of nodes linked by arrows. The nodes represent events or states of affairs, and the arrows represent causal connections between those events. When an event has two independent contributing causes, it is shown in a DAG as a node where two arrows ‘collide’. This is shown in Figure 1 above, where being admitted to Ward C has two contributing causes, from the two kinds of virus infection.
If we just look at a sample of cases in which the event at a collider happens, we’ll often see a correlation between the two independent causes. It may look like these causes are influencing one another, but they are not. It is a selection artefact, as causal modellers say. That’s collider bias. The correlation stems from the way in which the event at the collider depends on the two causes – in our simple example, it needed one cause or the other.
We want to take collider bias in the direction of physics – ultimately, in the direction of the experiments for which Aspect, Clauser and Zeilinger won their Nobel Prize. We want to propose an explanation for what may be going on in those experiments, and other cases of quantum entanglement.
We’ll get there via a series of toy examples. For the first of them, imagine that two physicists, Alice and Bob, play Rock, Paper, Scissors. For anyone who doesn’t know the rules of this game, at every turn, Alice and Bob each choose one of these three options, and send their calls to a third observer, Charlie. As in the usual version of the game, rock beats scissors, scissors beats paper, and paper beats rock. Charlie makes a list of the results: Alice wins, Bob wins, or it’s a draw.
Suppose that Charlie likes Alice and dislikes Bob. He therefore follows the policy of throwing away most of the results when Bob wins. In the remaining ‘official’ results, Alice wins a lot more often than Bob. The correlation looks the way it would if Alice actually had some influence over Bob’s choice – as though Alice choosing scissors makes it a lot less likely that Bob will choose rock, and so on. If Alice and Bob are far apart, this could look like Schrödinger’s magic. But there’s no real Alice-to-Bob causation involved. It is just collider bias at work. Given Charlie’s policy, the event at the collider – whether he retains or throws away the result – is influenced both by Alice’s choice and by Bob’s choice, giving us the same kind of converging arrows as in Figure 1 above.
Suppose that in a particular round of the game Alice chooses paper and Bob chooses rock. As in the medical case, Alice would be making a mistake if she says: ‘If I had chosen scissors instead, Bob would probably not have chosen rock.’ The right thing for her to say is: ‘If I had chosen scissors, then Charlie would probably have discarded the result – so my choice may have made a difference to Charlie’s decision, but it didn’t make a difference to Bob’s choice.’
Now to our second ingredient. It is the least familiar of all, although it, too, is already on the shelf, if you know where to look. It doesn’t have an established name, outside of our own work. We call it constraining a collider. We’ll use the Rock, Paper, Scissors game to explain what it is.
In the version of the game just described, Charlie could favour Alice only by discarding some results. Let’s see what happens if we rig the game in Alice’s favour, without throwing any results away. In our world, this isn’t going to happen naturally so, for now, let’s imagine it happening supernaturally. Suppose God also likes Alice more than Bob, so he tweaks reality to give her an advantage. Perhaps he arranges things so she never loses when she plays the game on Sundays.
How does God do it? It doesn’t matter for our story, which doesn’t need to be realistic at this point, but here’s one possibility. In a so-called ‘deterministic’ universe, everything that happens is determined by the initial conditions at the very beginning of time. If God gets to choose the initial conditions, and (relying on his divine foreknowledge) knows exactly what follows from them, he can simply choose the initial conditions so that Alice never loses on Sundays.
Readers who prefer a God-free version could imagine that Alice and Bob live in a simulation, and that the artificial superintelligence (ASI) that runs the simulation favours Alice on Sundays. Some serious thinkers have suggested that we ourselves may live in a simulation, so it would be hasty to say that this version is inconceivable.
On Sunday Alice can’t lose, so if she had chosen scissors, Bob could not have chosen rock
Now we can explain our terminology. In a case like this, we say that God (or the ASI) constrains the collider – just on Sundays, in this version of the story. A collider is constrained if something prevents some of the possibilities that would normally be allowed (such as Bob winning, in our example).
To see what difference this makes, think about a round of the game where Alice chooses paper and Bob chooses rock. Is Alice still making a mistake if she says: ‘If I had chosen scissors instead, Bob would not have chosen rock’?
It now depends what day of the week it is. This is still a mistake on Monday through to Saturday. On those days, the right thing for Alice to say is: ‘If I had chosen scissors, Bob would still have chosen rock (and I would have lost).’ But Sunday is different. On Sunday Alice can’t lose, so if she had chosen scissors, Bob could not have chosen rock.
Let’s suppose that Alice knows that the game works this way. Perhaps she figured it out after years of experiments, and now makes a comfortable living as a gambler, working one day a week. From her point of view, it looks like she can control Bob’s choices (though only on Sundays). By choosing scissors, she can prevent Bob from choosing rock, and so on.
With a constrained collider, then, we would have something that looks a lot like causation across the collider, from one of the pair of incoming causes to the other. True, it would be a very strange kind of causality. For one thing, it would work the other way, too, from Bob to Alice (though less happily, from his point of view). By choosing rock on a Sunday, Bob could prevent Alice from choosing scissors, and so on.
For our purposes, it isn’t going to matter whether this would be real causality, or even whether the question makes sense. Could we still speak of both Alice and Bob as making free choices, for example, if the choices are linked in this way?
We think that entanglement itself is connection across a constrained collider
We take the following lesson from the example above: if natural causes constrained a collider, we should expect to find a new kind of dependence between the normally independent causes that feed into that collider. We call this new kind of relation connection across a constrained collider (CCC).
As we said, we invented the term ‘constrained collider’. As far as we know, the idea hasn’t been explicitly discussed before, in physics or in causal modelling. But it is already on the shelf, in the sense that there’s at least one place in physics where what we’re calling CCC has actually been proposed: it has been suggested as a key for solving the so-called black hole information paradox by the physicists Juan Maldacena and Gary Horowitz.
The background here is that Stephen Hawking discovered a process now called Hawking radiation, by which all black holes eventually evaporate away to nothing. He thought initially that this process would be random, preventing the escape of information that had fallen into the black hole in the first place. Some physicists disagreed, and in 1997, with Kip Thorne and John Preskill, Hawking made a public bet on the matter. Hawking and Thorne took one side (against the escape of information), and Preskill the other. (Hawking eventually conceded that Preskill had won.)
In 2004, Maldacena and Horowitz proposed a new way for information to escape from a black hole. In our new terminology, they suggested that a collider inside the black hole is constrained by a special ‘final state boundary condition’ at that point. They suggest that this creates a zig-zag causal path through time, along which information can escape from a black hole. In our terms, that would be a connection across the constrained collider.
Discussing the Maldacena-Horowitz hypothesis in 2021, the Cambridge physicist Malcolm Perry said:
The interior of the black hole is therefore a strange place where one’s classical notions of causality … are violated. This does not matter as long as outside the black hole such pathologies do not bother us.
Our proposal is that ‘such pathologies’ are exactly what’s been bothering us in QM, ever since 1935. We think that entanglement itself is connection across a constrained collider. To explain how that can be the case, and to introduce our two remaining ingredients, we need to get closer to the physics of the quantum world.
As noted, many Bell experiments have now confirmed the strange correlations, predicted by QM showing the quantum world is unavoidably nonlocal. Given that these so-called Bell correlations were important enough to win Nobel Prizes, readers may be surprised to learn that they can easily be reproduced in a version of our Rock, Paper, Scissors game. The only change we need is to have Alice and Bob each flip a coin before they make their choice.
In this variant – let’s call it quantum Rock, Paper, Scissors – Alice and Bob each send two pieces of information to Charlie: their choice of rock, paper or scissors, and the result of their coin flip. So Charlie gets four values, two choices and two coin outcomes. This is precisely the same amount of information generated in each run of a Bell experiment.
In quantum Rock, Paper, Scissors, it is very easy for Charlie to set up a filter, keeping some results and throwing away others, to make sure that the set of results he keeps satisfies the Bell correlations. By using the right filter, Charlie can ensure that the selected results look exactly like the data generated in real Bell experiments. To match one kind of Bell experiment, for example, Charlie’s filter specifies that, when the settings are the same, the two outcomes must be different; and that, when the settings are different, the outcomes are the same 75 per cent of the time.
This doesn’t mean that there is any sort of strange nonlocal magic in quantum Rock, Paper, Scissors, of course. As in the earlier version, the correlations are simply a selection artefact, a result of collider bias.
There is one big difference between quantum Rock, Paper, Scissors and real Bell experiments
We could reintroduce God or an ASI at this point, to add a constrained collider to quantum Rock, Paper, Scissors. There would be one interesting difference from the original game. In that case, the effect of the constraint was to give Alice and Bob control over each other’s choices, making it hard to maintain that they both had freedom to choose. In quantum Rock, Paper, Scissors, as in the analogous real Bell experiments, that problem goes away: Alice and Bob each get some influence over the result of the other’s coin toss, but we can still treat both of their own choices as completely free.
There is one big difference between quantum Rock, Paper, Scissors and real Bell experiments, however, that we haven’t yet mentioned. In quantum Rock, Paper, Scissors, Alice and Bob send their choices to Charlie after they are made. In a spacetime diagram with time running up the vertical axis, the structure looks like an upside-down letter V – see the left-hand side of Figure 2 below. We’ll say that cases like this are ‘∧-shaped’.
In real Bell experiments, Alice and Bob receive their particles from the source, which emits them earlier in time. So the structure looks like ∨, as in the right-hand side of Figure 2 – we’ll say that they are ‘∨-shaped’.

Figure 2: the difference between ∧-shaped and ∨-shaped experiments
Can we flip quantum Rock, Paper, Scissors to make it ∨-shaped as well? It might look easy. We can have Charlie toss the two coins and send them to Alice and Bob, so that the results (heads or tails) become Alice and Bob’s measurement outcomes.
But if that’s all we do, Charlie won’t know what choices Alice and Bob are going to make when he sends out the coins. That means there’s no way for him to put bias into the results, in the way that he could in the ∧-shaped case. There’s no way that Charlie can produce the Bell correlations, in other words.
But suppose we let Charlie know in advance what choices Alice and Bob are going to make – we give him a crystal ball, say. Then it is very easy for him to manage the coins so that the net results, gathered over many plays of the game, satisfy the Bell correlations. The trick is for Charlie to toss one coin, and then choose the result for the other coin based on a rule that takes into account Alice and Bob’s future choices. The rule he needs is the same as in the ∧-shaped version of the game. When Alice and Bob’s settings are the same, he sends them different coin results; when the settings are different, he sends the same coin results 75 per cent of the time.
Let’s ask the same question we did about the ∧-shaped version. Does the new ∨-shaped case involve some kind of nonlocal magic from Alice to Bob, and vice versa?
We hope that readers will be inclined to say ‘No’ to this question. After all, the basic causal structure of the new ∨-shaped version is something like Figure 3 below. Thanks to Charlie’s crystal ball and the preset rules, Alice’s and Bob’s choices both influence Charlie’s outcomes, in every case. This means that Charlie’s selection procedure is a collider, and we have to be on our guard for collider bias.

Figure 3: a past collider
For this reason, attentive readers might suspect that collider bias plays the same role in explaining the results of the new ∨-shaped quantum Rock, Paper, Scissors as it did in the ∧-shaped case. But there’s one very big difference between these two cases – which brings us to our third ingredient – something we call ‘initial control’.
In the ∧-shaped version of quantum Rock, Paper, Scissors, Charlie had to throw away results he didn’t want. But in the ∨-shaped case, he gets to choose the results in light of what he learns from the crystal ball. He’s arranging the coins in exactly the pattern he wants, not achieving the pattern by discarding a lot of cases that don’t fit. In this case, then, Charlie himself can constrain the collider, no gods or ASI needed.
What Charlie needs to do this is an ordinary ability we take for granted, to control the so-called ‘initial conditions’ – the way things are set up at the beginning of the experiment. This familiar ability is our third ingredient. Let’s call it initial control.
Perhaps we shouldn’t take initial control for granted. It is actually a remarkable ability, one that depends on the fact that we live in a place where abundant energy can be harnessed by creatures like us to do work. Living on a cool planet next to a hot star is much like living at the base of a giant waterfall. It’s easy to harness the passing flow of energy, just as life on Earth has been doing for billions of years.
Like all the complicated ways in which terrestrial creatures control their environment, the ability of human scientists to control experiments depends on harnessing this energy flow. But, like the natural flow of heat between different-temperature objects, it works only one way. We have much more control over the initial conditions of experiments than over their final conditions. It’s easy to arrange the balls on a pool table into precise positions before the initial break, for example, but virtually impossible to play the game so that they all end up in those positions.
It doesn’t have the relativity-challenging character normally associated with Schrödinger’s magic
The combination of the collider structure in Figure 3 above and the constraint provided by initial control gives us CCC – connection across the collider. If we are happy to use causal language, we can say that it gives us the kind of zig-zag causal connection shown in Figure 4 below. There’s also a zig-zag path from Bob’s choice to Alice’s outcome, of course.

Figure 4: the Parisian Zig Zag
But does ∨-shaped quantum Rock, Paper, Scissors involve some kind of nonlocal magic from Alice to Bob, and vice versa? At this point, we need to be careful about what we mean by nonlocality. As we have just seen, there is indeed some influence, or connection, from Alice to Bob, and vice versa – it is CCC. Since they are at a distance from each other, and a direct connection might need to be faster than light, we might still want to call it nonlocality. (One of last year’s Nobel laureates told us he thought such a zig zag should still count as a nonlocal effect.)
However, the connection between Alice and Bob is indirect, and depends entirely on processes that don’t themselves require anything faster than light. So, whatever we call it, it doesn’t have the relativity-challenging character normally associated with Schrödinger’s magic. And it is not very mysterious: we know exactly what it is, namely, connection across a constrained collider.
The crystal balls were magic, of course, but, once we gave ourselves those, the explanation of the connection between Alice and Bob is straightforward. Imagine if something like this could explain the results of real Bell experiments – that would be a nail in the coffin of the quantum spooks.
To make this work, we need our final ingredient. It is retrocausality, the idea that causality might work backwards in time, from future to past. In ∨-shaped quantum Rock, Paper, Scissors, we gave Charlie a crystal ball, to allow causation to work backwards – in other words, to allow Alice and Bob’s choices to feed into the rule Charlie uses to select the measurement outcomes.
This zig-zag path would avoid the kind of faster-than-light magic that Einstein and Schrödinger objected to
In the real world, of course, we don’t find magical crystal balls on any actual shelf. In the quantum world, however, retrocausality is an old and familiar idea. In that sense, it is certainly available off the shelf. It was first proposed in the late 1940s by the Parisian physicist Olivier Costa de Beauregard. He was a graduate student of the French physicist Louis de Broglie, another of the 1920s pioneers. In his own PhD thesis in 1924, de Broglie had proposed that all particles can behave like waves. Just five years later, after experiments had confirmed it, this won him the Nobel Prize.
Costa de Beauregard spotted a loophole in the Einstein-Schrödinger argument from 1935. Schrödinger had said that ‘measurements on separated systems cannot affect one another directly, that would be magic’. Costa de Beauregard pointed out that they might affect each other indirectly, via the kind of zig-zag path shown in Figure 4 above. (That’s why we called it the Parisian Zig Zag.)
This zig-zag path would avoid the kind of faster-than-light magic that Einstein and Schrödinger objected to. But it would still undermine the Einstein-Schrödinger argument against Bohr. If the reality on Bob’s side of the experiment can depend on Alice’s choice of measurement, we’re not entitled to assume that it would have been there anyway, even if Alice had done something else.
Later, after Bell’s work in the 1960s, Costa de Beauregard proposed that the zig zag could explain the strange Bell correlations, without relativity-threatening nonlocality.
Retrocausality remained a niche idea in QM for many years, though it has long had some distinguished proponents. In the 1950s, one of them, at least briefly, was the British physicist Dennis Sciama, who taught an astonishing generation of physicists, including Hawking. Sir Roger Penrose, himself a recent Nobel laureate, has long been sympathetic to the idea, as he argued in his chapter for the collection Consciousness and Quantum Mechanics (2022), edited by Shan Gao. There’s a story from the 1990s of Penrose drawing a zig zag at a quantum workshop at the Royal Society in London, and joking: ‘I can get away with proposing this kind of thing, because I’m already a Fellow here.’ (Now that he has a Nobel Prize, it is even easier, presumably!)
More recently, we ourselves have written about the advantages of retrocausal approaches to QM, both in avoiding action at a distance, and in respecting ‘time-symmetry’, the principle that the microworld doesn’t care about the distinction between past and future. But an additional striking advantage of retrocausality seems to have been missed. It suggests a simple mechanism for ‘the characteristic trait of quantum mechanics’ (Schrödinger), ‘its weirdest feature’ (Weinberg) – in other words, for the strange connections between separated systems called quantum entanglement.
Starting with retrocausality, our recipe goes like this, in four easy steps:
- Retrocausality automatically introduces colliders into Bell experiments, at the point where the two particles are produced. Alice and Bob’s choices of measurement both feed back into the past, to influence the particles at this point.
- That’s interesting because colliders produce collider bias and causal artefacts – correlations that look like they involve causation, but really don’t.
- But constraining a collider can turn a causal artefact into a real connection across the collider, as shown in Figure 4. Because of the constraint, a different choice on Alice’s side sometimes requires a different outcome on Bob’s side, and vice versa.
- In the case of colliders in the past, as in Figure 3, constraint is easy. It just follows from normal initial control of experiments.
Taken together, these steps suggest a simple explanation for the Parisian Zig Zag, and the strange connections in the quantum world required by entanglement: it is connection across constrained colliders, where the colliders result from retrocausality and the constraints from ordinary initial control of experimental setups.
We don’t mean that it is a trivial step from ∨-shaped quantum Rock, Paper, Scissors to real Bell experiments. But this toy example demonstrates that the combination of retrocausality and initial control can give rise to a connection between separated systems that looks very similar to entanglement. In our view, this is such a striking fact – and entanglement is otherwise such a strange and mysterious beast – that we propose the following hypothesis:
Hypothesis: quantum entanglement is connection across constrained colliders (CCC), where the colliders result from retrocausal influence on the source of pairs of entangled particles, and the constraint results from normal initial control of the experiments that produce such particles.
If this hypothesis turns out to be true, then in place of Schrödinger’s magic we’ll get something that works like Costa de Beauregard’s zig zag. That’s just what connection across a constrained collider does: it makes a zig zag from two converging arrows.
It will still be true that QM gives us a new kind of connection between the properties of distant systems. Bell experiments provide very convincing evidence that quantum entanglement is a real phenomenon. But it would no longer look mysterious – any world that combines retrocausality and initial control would be expected to look like this.
QM has been built on the idea that there are limits to what it is possible to know about physical reality
Finally, a note for readers who are worried that the cure is worse than the disease – that retrocausality opens the door to a menagerie of paradoxes and problems. Well spotted! For one thing, the crystal balls give Charlie options much like those of the famous time-traveller, meeting his own grandfather long before his parents met. What’s to stop him from interfering with the course of history, say by bribing Bob to make a different choice than the one shown in the crystal ball? (In the causal loop literature, this is called ‘bilking’.)
Also – less dramatic, maybe, but especially interesting in comparison to QM – the crystal balls allow Alice and Bob to send messages to Charlie, and hence potentially, with his help, to signal to each other. This isn’t possible in real Bell experiments, where Alice and Bob can’t signal to each other, despite having some influence on each other’s measurement outcomes. So isn’t this bad news for retrocausality?
These are good objections, but it is easy to modify the ∨-shaped quantum Rock, Paper, Scissors game to avoid them. We just need to split Charlie’s functions into two parts. Most of what he does gets replaced by a simple algorithm, inside a black box, that takes in information about the two future measurement settings, and spits out the two measurement outcomes.
Charlie himself can’t see inside the black box, and doesn’t have access to the future settings. But he still has a vital job to do. The box has a knob on the front, with a small number of options. Charlie controls that knob, and if he wants the device to produce the Bell correlations, he needs to choose the right option. In the terminology of QM, that’s called ‘preparing the initial state’.
If that’s all that Charlie does, and the quantum black box takes care of the rest, the door to the menagerie is closed. Alice and Bob can no longer signal to Charlie, or to each other. Everything works as in orthodox QM, except that we now have the prospect of an explanation for entanglement.
This means that if nature wants retrocausality without signalling into the past, and the paradoxes it would lead to, it needs black boxes – places in nature where observers like Charlie can’t see the whole story. In normal circumstances, such black boxes would seem like another kind of magic. Charlie is a clever guy, after all. What’s to stop him from taking a peek inside?
The answer, in the quantum case, is Heisenberg’s uncertainty principle, from 1927. Ever since then, QM has been built on the idea that there are limits to what it is possible to know about physical reality. This is just the veil of ignorance we need, to allow retrocausality in QM without threatening anybody’s grandparents. As Adam Becker put it in the New Scientist in 2018:
Heisenberg’s uncertainty principle states that it is impossible to know both the position and momentum of a particle at the same time. So there are features of the quantum world that are persistently hidden from us, and this is ultimately what allows for retrocausation without letting us send signals to the past.
It may seem just too convenient, that one curious feature of quantum theory allows a paradox-free version of another curious feature. But in the real world, every piece of stage magic has a coherent explanation underneath. Often that explanation combines various components in surprising ways: stage magic wouldn’t be magic if it was obvious how it worked.
We’ve seen that quantum entanglement looked like magic, by the standards of some of the pioneers who discovered it. It still looks very strange, even to the physicists who have just won Nobel Prizes for proving that it is real. Any coherent explanation of it seems likely to combine some unexpected elements, and to require a careful analysis of how causes interact with each other, down at the level where we can’t see all the effects. The biggest surprise, in our view, is how few ingredients the explanation seems to need – and how simple the recipe is for putting them together.






