What does it mean to know mathematics? Since maths is something we teach using textbooks that demand years of training to decipher, you might think the sine qua non is intelligence – usually ‘higher’ levels of whatever we imagine that to be. At the very least, you might assume that knowing mathematics requires an ability to work with symbols and signs. But here’s a conundrum suggesting that this line of reasoning might not be wholly adequate. Living in tropical coral reefs are species of sea slugs known as nudibranchs, adorned with flanges embodying hyperbolic geometry, an alternative to the Euclidean geometry that we learn about in school, and a form that, over hundreds of years, many great mathematical minds tried to prove impossible.
Sea slugs have at least the rudiments of brains; they generally possess a few thousand neurons, whose large size has made these animals a model organism for scientists studying basic neuronal functioning. This tiny number isn’t nearly enough to enable the slug to formulate any representation of abstract signs, let alone an ability to mentally manipulate them, and yet, somehow, a nudibranch materialises in the fibres of its very being a form that genius-level human mathematicians didn’t discover until the 19th century; and when they did, it nearly drove them mad. In this instance, complex brains were an impediment to understanding.
Nature’s love affair with hyperbolic geometry dates to at least the Silurian age, more than 400 million years ago, when sea floors of the early Earth were covered in vast coral reefs. Many species of corals, then and now, also have hyperbolic structures, which we immediately recognise by the frills and crenellations of their forms. Although corals are animals, they have only very simple nervous systems and can’t be said to have a brain. A head of coral is actually a colonial organism made up of thousands of individual polyps growing together; collectively, they grow a vascular system, a respiratory system and a crude gastrointestinal system through which all the individuals of the colony eat and breathe and share nutrients. Nothing like a brain exists, and yet the colony can organise itself into a mathematical surface disallowed by Euclid’s axiom about parallel lines. Strike two against ‘higher intelligence’.
Ask any fifth-grader what the angles of a triangle add up to, and she’ll say: ‘180 degrees’. That isn’t true on a hyperbolic surface. Ask our fifth-grader what’s the circumference of a circle and she’ll say: ‘2π times the radius’. That’s also not true on a hyperbolic surface. Most of the geometric rules we’re taught in school don’t apply to hyperbolic surfaces, which is why mathematicians such as Carl Friedrich Gauss were so disturbed when finally forced to confront the logical validity of these forms, and hence their mathematical existence. So worried was Gauss by what he was discovering about hyperbolic geometry that he didn’t publish his research on the subject: ‘I fear the howl of the Boetians if I make my work known,’ he confided to a friend in 1829. To their universal horror, other mathematicians soon converged on the same conclusion and the genie of non-Euclidean geometry was let loose.
But can we say that sea slugs and corals know hyperbolic geometry? I want to argue here that in some sense they do. Absent the apparatus of rationalisation and without the capacity to form mental representations, I’d like to postulate that these humble organisms are skilled geometers whose example has powerful resonances for what it means for us humans to know maths – and also profound implications for teaching this legendarily abstruse field.
I’m not the first person to have considered the mathematical capacities of non-sentient things. Towards the end of Richard Feynman’s life, the Nobel Prize-winning physicist is said to have become fascinated by the question of whether atoms are ‘thinking’. Feynman was drawn to this deliberation by considering what electrons do as they orbit the nucleus of an atom. In the earliest days of atomic science, atoms were conceived as little solar systems with the electrons orbiting in simple paths around their nuclei much as a planet revolves around its sun. Yet in the 1920s, it became evident that something much more mathematically complex was going on; in fact, as an electron buzzes around its nucleus, the shape it makes is like a diffused cloud. The simplest electron clouds are spherical, others have dumbbell and toroidal shapes. The form of each cloud is described by what’s called a Schrödinger equation, which gives you a map of where it’s possible for the electron to be in space.
Schrödinger equations (after the pioneering quantum theorist Erwin Schrödinger and his hypothetical cat), are so complicated that, when Feynman was alive, the best supercomputers could barely simulate even the simplest orbits. So how could a brainless electron be effortlessly doing what it was doing? Feynman wondered if an electron was calculating its Schrödinger equation. And what might it mean to say that a subatomic particle is calculating?
Electrons don’t follow mathematical instructions any more than Jimi Hendrix followed a musical score
The world is full of mundane, meek, unconscious things materially embodying fiendishly complex pieces of mathematics. How can we make sense of this? I’d like to propose that sea slugs and electrons, and many other modest natural systems, are engaged in what we might call the performance of mathematics. Rather than thinking about maths, they are doing it. In the fibres of their beings and the ongoing continuity of their growth and existence they enact mathematical relationships and become mathematicians-by-practice. By looking at nature this way, we are led into a consideration of mathematics itself not through the lens of its representational power but instead as a kind of transaction. Rather than being a remote abstraction, mathematics can be conceived of as something more like music or dancing; an activity that takes place not so much in the writing down as in the playing out.
Music gives us a rich analogy by which to consider the idea of mathematics as performance, for you don’t need to be able to write down music to be a musician. Maybe if you want to play Mozart, but not in many other cases. Most folk music throughout history has been created by people who are sonically illiterate. Elvis Presley, Michael Jackson, Eric Clapton and Jimi Hendrix all claimed not to read music. In a British TV interview, Paul McCartney said: ‘As long as the two of us know what we’re doing, ie, John and I, we know what chords we’re playing and we remember the melody, we don’t actually ever have the need to write it down or read it.’
Indian classical music, easily as complex as the Western classical cannon, is based on ragas that were generally transmitted aurally from master to student, not traditionally written down. In this millennia-old practice, music is recognised as an innately mathematical form: the Sanskrit word prastara means the ‘study of mathematically arranging’ ragas and rhythms into pleasing compositions. Ragas certainly can be written down (indeed, Indian musical notation dates back more than 2,000 years), and mathematics can be notated, but it doesn’t have to be. There are lots of things doing maths without a formal script, and I’d argue that it makes no sense to say that electrons or sound waves are following mathematical instructions any more than it makes sense to say that Jimi Hendrix was following a musical score. The possibility of writing down music is something apart from its performance, and maths can be considered in a similar way. In short, the notation isn’t the act.
Among my favourite mathematical performers are holograms, which enact a gorgeous operation called the Fourier transform. This extraordinarily complex, elegant equation is named in honour of Joseph Fourier, a mathematician and physicist who advised Napoleon and discovered what we now call the greenhouse effect (he called it the ‘hotbox’ effect). The Fourier transform has been called the most useful piece of mathematics of all time; you rely on its power every time you make a cellphone call or listen to a piece of digitally recorded music. Music synthesis also results from clever applications of Fourier’s equations. We’ll get to the audio part in a moment, but first let’s look at the visual face of this mathematical marvel.
Holograms differ from photographs in a fundamental way: a photo captures a two-dimensional rendering of light and shade and colour, like a very detailed painting; meanwhile, when light shines through a holographic plate, it assembles into a three-dimensional replica of the original object, recreating in light a simulacra of that thing. The image you see with a hologram is sculptural, really occupying 3D space, so you can move around and view it from different angles. Yet when you look at a holographic plate, there’s no image at all, just a blur in which you may be able to discern speckled rings and dots. What’s been captured on the plate is the Fourier transform of the object, which encodes more information and a different kind of information than a photo can.
Every object has a Fourier transform, and in theory we could calculate the transform of any object we desire and make a holographic plate to generate its form even though an actual physical object never existed. The emerging field of computer-generated holography (CGH) is trying to do just this. If it can be made to work, it will revolutionise computer games and animation; we’d be able to watch whole movies akin to the marvellous holographic projection of Princess Leia in the original Star Wars film.
Calculating transforms for complex objects requires vast computational powers and skills as yet unachieved by human CGH practitioners. Nonetheless, simple chemicals interacting with light on a piece of film manage to enact Fourier transforms of complicated scenes. Acting together, wave fronts of light and atoms execute a beautiful piece of mathematical encoding, and when the light plays back through the film they do the de-encoding. As such, where a photograph is a representation, a hologram is a performance.
Fourier came to his equation in the early 1800s, not to describe images (the origin of holograms dates to the 1940s), but to describe heat flow, and it turns out that his mathematics also leads to enormously powerful applications in the audio domain. Why does a piece by Mozart sound so different when played on a flute or a violin? One way of explaining it is that, although both instruments are playing the same sequence of notes, the Fourier transform of the sound produced by each one is different. The transform reveals the sonic DNA of the instrument’s sound, giving us a precise description of its harmonic components (formally, it describes the set of pure sine waves that make up the sound.) With software, audio engineers can analyse the transform of a musical recording and tell you what kind of instrument was playing; moreover, they can tweak the transform to bring out qualities they like and filter out ones they don’t. By fiddling with the maths, one can sculpt the sound to suit particular tastes.
Calculating Fourier transforms of sounds is a lot easier than calculating the transforms of visual scenes, and software engineers have created programs to simulate musical instruments (eg, Apple’s GarageBand), effectively giving users a sim-orchestra on their laptops for the price of an app. Advances in Fourier-based sound simulation have revolutionised the economics of the music business including movie scoring. Now you don’t need an actual orchestra to produce stirring strings to accompany a heroine’s triumph, you can conjure them from the virtual depths, generated through mathematics.
From my perspective, even the chairs can be said to be participating in the mathematical performance enacted in a concert hall
While music synthesis demonstrates how we can employ mathematics to create something powerful out of a vacuum, here I’m more interested in what happens in actual concert halls. Great halls have their own unique ‘sound’, with each room acting as a filter for the music, tweaking and sculpting its Fourier transform. Contemporary acoustic engineers use Fourier techniques when designing new concert halls, manipulating the architecture of the space, for example adding baffles in specific places, all aided by software that simulates how sounds will react within the space. If the engineers do their job well, there will be no ‘dead spots’ and the hall will sing with warmth and resonance. Here we have a mathematical performance between the sound waves, the architecture, and the surfaces of the walls.
Some music schools now have electronic ‘practice rooms’ where, through software, you can dial up a Fourier-based simulation of a cathedral or a tin shed and hear what your playing would sound like in different spaces. However, music connoisseurs will tell you that no sim is a substitute for physical reality, which is why revered concert halls, such as Vienna’s Musikverein, or New York’s Carnegie, won’t be replaced by software any time soon. It’s interesting that most of the best-rated halls were built before 1901, a fact that the acoustic legend Leo Beranek has attributed to their lack of fancy architecture (their resolutely shoe-box shape) and their lightly upholstered seats. From the perspective I’m adopting, even the chairs can be said to be participating in the mathematical performance enacted in a concert hall. Score another home run for non-sentience.
Since at least the time of Pythagoras and Plato, there’s been a great deal of discussion in Western philosophy about how we can understand the fact that many physical systems have mathematical representations: the segmented arrangements in sunflowers, pine cones and pineapples (Fibonacci numbers); the curve of nautilus shells, elephant tusks and rams horns (logarithmic spiral); music (harmonic ratios and Fourier transforms); atoms, stars and galaxies, which all now have powerful mathematical descriptors; even the cosmos as a whole, now represented by the equations of general relativity. The physicist Eugene Wigner has termed this startling fact ‘the unreasonable effectiveness of mathematics’. Why does the real world actualise maths at all? And so much of it? Even arcane parts of mathematics, such as abstract algebras and obscure bits of topology often turn out to be manifest somewhere in nature. Most physicists still explain this by some form of philosophical Platonism, which in its oldest form says that the universe is moulded by mathematical relationships which precede the material world. To Platonists, matter is literally in-formed, and guided by, a pre-existing set of mathematical ideals.
In the Platonic way of seeing, matter (the stuff of everything) is rendered inert, stripped of power and subordinated to ethereal mathematical laws. These laws are given ontological primacy with matter being effectively a sideline to the ‘true reality’ of the equations. Over the past half-century, this vision has been updated somewhat because now matter, or subatomic particles, have themselves been enfolded into the equations. Matter has been replaced by fields – as in electric and magnetic fields – and now it’s the fields that follow the laws. Still, it’s the laws that retain primacy and power; hence the obsession with finding an ultimate law, a so-called ‘theory of everything’.
Platonism has always bothered me as a philosophy in part because it’s a veiled form of theology – mathematics replaces God as the transcendent, a priori power – so if we want to articulate an alternative, we need new ways of interpreting mathematics itself that don’t also slip into deistic modes. Thinking about maths as performative points a way forward, while also offering a powerful pedagogic model.
Corals and sea slugs construct hyperbolic surfaces and it turns out that humans can also make these forms using iterative handicrafts such as knitting and crochet – you can do non-Euclidean geometry with your hands. To crochet a hyperbolic structure, one just increases stitches at a regular rate by following a simple algorithm: ‘Crochet n stitches, increase one, repeat ad infinitum.’ By increasing stitches, you increase the amount of surface area in a regular way, visually moving from a flat or Euclidean plane into a ruffled formation that models the ‘hyperbolic plane’. Mathematically speaking, the hyperbolic plane is the geometric opposite of the sphere: where the surface of a sphere curves towards itself at every point, a hyperbolic surface curves away from itself. We can define these different surfaces in terms of their curvature: a Euclidean plane has zero curvature (it’s flat everywhere), a sphere has positive curvature, and a hyperbolic plane has negative curvature. In this sense, it is a geometric analogue of a negative number.
Knitting, crochet and weaving were the original digital technologies: their algorithmic ‘patterns’ are literally written in code
Just as geometric relationships on a sphere are different to those on a flat plane – think of what you know about the surface of the Earth versus a flat piece of paper – so, they are different again on a hyperbolic surface. Whereas on a flat plane the angles of a triangle add up to 180 degrees, on a sphere they add up to more, and on a hyperbolic surface they add up to less. It’s hard to appreciate this abstractly when you learn it from textbooks, as I did at university, but you can demonstrate it materially on a crocheted hyperbolic plane by stitching triangles onto the surface. You can also demonstrate visually that parallel lines diverge and other apparent absurdities. If Gauss had known how to crochet he mightn’t have been driven so bonkers.

Crochet Coral Reef by Margaret and Christine Wertheim and the Institute For Figuring. Photo © IFF
It took a woman, the mathematician Daina Taimina at Cornell University, to discover hyperbolic crochet and to give mathematicians a tangible model of this form. I have conducted workshops about this with women all over the world delighting in how much geometry can be conveyed through acts of making. There’s also a link here with general relativity, because the discovery of the hyperbolic plane opened up a whole new era in geometric thinking, leading ultimately to generalised Riemannian geometry, which can describe any complexly curved surface, and is the mathematics underlying Albert Einstein’s equations for the cosmos.
Via handicrafts, we can introduce people to concepts about curved spacetime and multidimensional manifolds, leading with our fingers, and out to questions about measuring the structure of the cosmic whole. We can see this as a form of ‘digital intelligence’, and it’s worth noting that iterated handicrafts (knitting, crochet, weaving) were the original digital technologies: their algorithmic ‘patterns’ are literally written in code. It’s no coincidence that computer punch cards were derived from the cards used in automated looms. Here, knowing emerges from hands performing mathematics: it is a kind of embodied figuring.
People talk about playing music but mathematics can also be a form of play. One way of thinking about maths is as a language of pattern and form, so when you play with patterns you are doing maths. A beautiful example of mathematical pattern-play can be seen with the great Islamic mosaicists who decorated mosques and palaces such as the Alhambra Palace in Granada in Spain with intricate tilings whose mathematical complexities are still a source of wonder.
Long before European geometers realised that there are only 17 mathematically distinct tessellations of the plane – different ways of filling an area with a regular tiling pattern – medieval mosaicists working with their hands using the Hasba method knew about them all. Moreover, medieval Islamic tilers had also discovered aperiodic tiling, which is a way of filling a plane where the pattern never repeats. Western mathematicians discovered these tilings only in the 1960s, again after centuries of theorising that such patterns were impossible. One of the magical qualities of aperiodic tilings is that they look simultaneously random and regular; as a geometric form of chaos, they are rule-based yet inherently unpredictable.

Mosaic tiling from the tomb of Hafez in Shiraz. Courtesy Wikipedia
At first, when Western mathematicians (Sir Roger Penrose among them) discovered aperiodic tilings, these formations were thought to be just a mathematical curiosity; like hyperbolic surfaces, they seemed to defy common sense so that no one imagined such things could be present in the physical world. Prejudice was so intense that when the Israeli chemist Dan Shechtman announced in 1982 that he’d created a new type of crystal with an aperiodic structure, many fellow scientists refused to believe him. (Like Gauss, he too delayed publishing because of the supposedly absurd nature of his claims.) Shechtman’s quasicrystals have brought about a paradigm shift in crystallography, in part because now we know that crystals can be chaotic, exhibiting order without repetition.

Aperiodic ‘Penrose’ tiling pattern. Courtesy Wikipedia
Lewis Carroll would have had a field day with this concept, which calls to mind the Red Queen’s exhortation to Alice that, with practice, one can ‘believe six impossible things before breakfast’. In 2009, after an intense search, a naturally occurring example of an aperiodic crystal was also found in the mineral icosahedrite. Strike three against intelligence as a prerequisite for doing mathematics.

Image of an aluminium-palladium-manganese quasicrystal surface. Courtesy Wikipedia
As a nice coda to this story, in 2011 Shechtman was awarded the Nobel Prize in chemistry.
Proof that studying equations isn’t the only path to mathematical insight also comes to us from Africa, where craftsmen discovered fractals centuries ago. A wide variety of fractal patterns are incorporated into African textiles, hairstyling, metalwork, sculpture, painting and architecture. One marvellous Ba-Ila village in southern Zambia is laid out in a fractal design reminiscent of the Mandelbrot set, that swirling icon of 1990s computer-graphic cool. In his book African Fractals: Modern Computing and Indigenous Design (1999), the mathematician Ron Eglash traces the story of the southern continent’s priority in a branch of geometry that came into Western consciousness only around the turn of the 20th century, and didn’t really flourish here until the development of computer graphics chips.
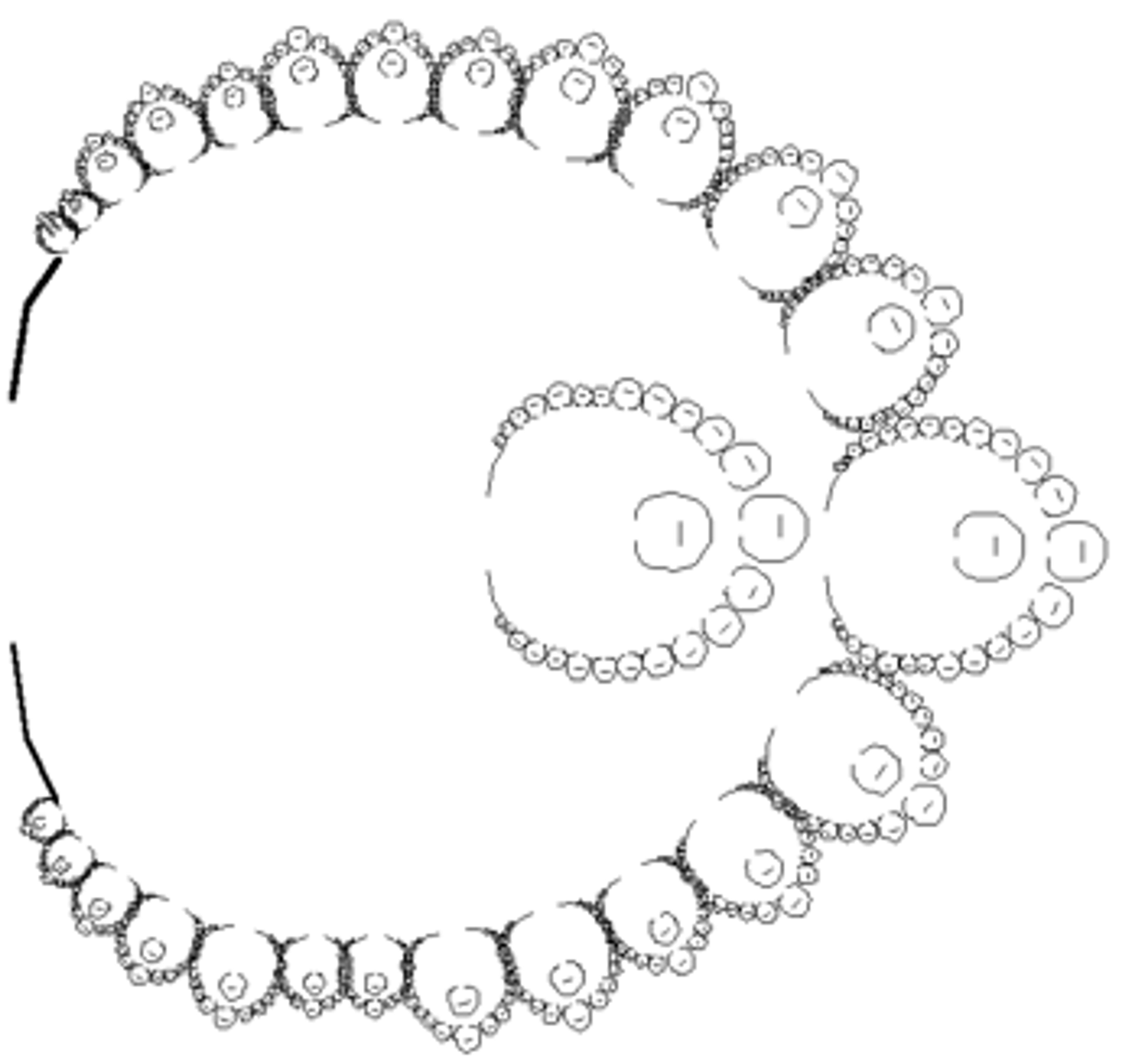
Fractal model for Ba-Ila village. From ‘African Fractals: Modern Computing and Indigenous Design’ by Ron Eglash
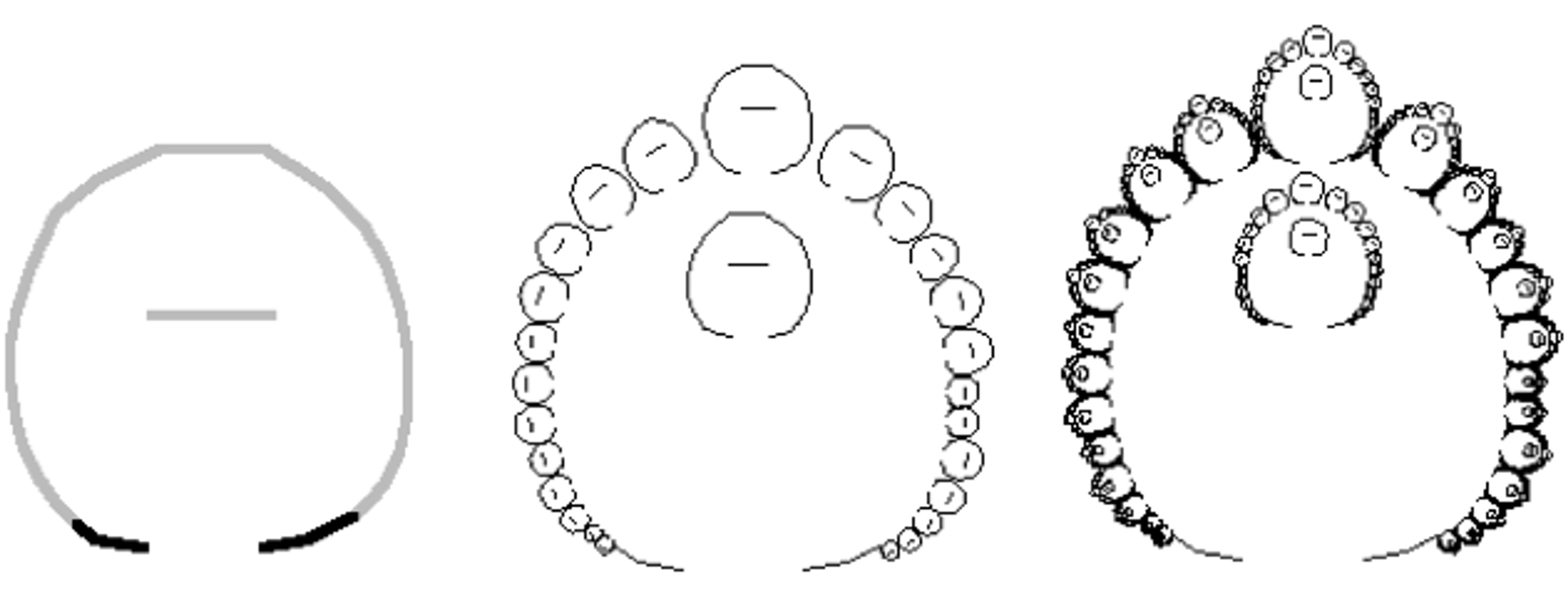
First three iterations of fractal model for Ba-Ila village. From ‘African Fractals: Modern Computing and Indigenous Design’ by Ron Eglash
Sea slugs do maths, electrons do maths, minerals do maths. Rainbows do an incredible mathematical performance when you take into account the primary and secondary bows, the dark band between them, and the red and green arcs of light under the primary bow. Next time you see a good rainbow, stop and take a look at the space around it, there’s so much going on; classical geometric optics doesn’t begin to capture its complexity. A stunning piece of mathematical performance is enacted by a peregrine falcon as it hurtles towards its prey; with its head held straight so it can fix one eye steadily on the quarry at a constant angle of 40 degrees, it swoops down at 200 mph in a perfect logarithmic spiral. Leonhard Euler’s 18th-century formula, with its unique mathematical properties, is enacted here by a bird.
All around us, nature is playing mathematical games and we too can join in the fun. Mathematics need not be taught as an abstraction, it can be approached as an embodied practice, like learning a musical instrument. This doesn’t invalidate what goes on in university classrooms or academic textbooks, since society needs professional mathematicians who can work with symbols, people such as Fourier and Bernhard Riemann who developed the maths that assists us to make cellphone calls, or determine the structure of the cosmos, and so much else besides. Because nature does so much mathematics, there will probably never be a time when professional ‘symbolising’ isn’t profoundly useful. In 2016, the Nobel prize in physics was awarded for ‘theoretical discoveries about topological phase transitions in matter’ – astonishing, complex work that emerged out of the discovery of another kind of supposedly impossible object (the quasi-particle) and whose mathematical insights might pave the way for quantum computers.
By thinking about mathematics as performance, we liberate it from the straightjacket of abstraction into which it has been too narrowly confined. If you ask professional mathematicians what they love about their work, a likely answer is its beauty. ‘Euclid alone looked on beauty bare’ wrote the poet Edna St Vincent Millay in 1923, while the mathematician André Weil (brother of Simone) claimed that solving a hard mathematical problem topped sexual pleasure.
The professionals know that mathematics swings; they delight in its playfulness, the plasticity of its forms, and (after some initial shock) the absurdities it throws up. Hyperbolic surfaces, aperiodic tilings, Möbius strips, negative numbers and zero all generated alarm at first, yet were ultimately embraced as gateways to new continents of mathematical wonder.
You don’t have to be a symbol-expert to appreciate this terrain. Just as humans are endowed with an ability to dance and play music (even if education too often crushes this out of us), so we have innate form-making and pattern-playing proclivities. Sea slugs, sound waves and falcons do mathematics; Islamic mosaicists and African architects do it too. So can you.